Calculating the load required to tip a table?

[william497]

I would like to understand the topic discussed in this thread more. https://www.physicsforums.com/threads/tipping-over-a-table-how-much-overhang.1012197/post-6598527

As I understand it, I can find the load required to tip the table can be calculated by this formula. L<W a/x
This is illustrated by this image.

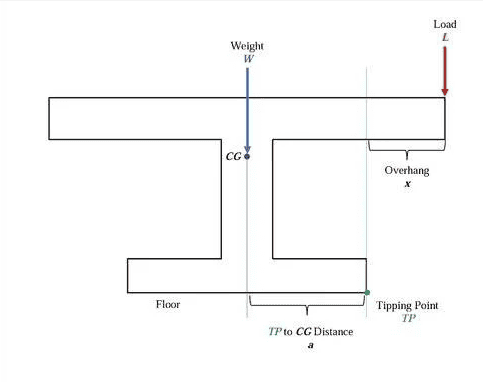
What I don't understand is this. If I have a base that weighs 50kg's and a top that weighs 5kg's, total weight acting downwards through the CG of 55kg. It will take a substantial load to tip the table.
If I have a base that weighs 5kgs and a top (same diameter) that weighs 50kg, same total weight, but I know it will be much easier to tip the table because it is top heavy.
I don't see how the equation allows for the changing height of the center of gravity.
Am I interpreting the equation correctly? Or does the equation need to be adjusted to allow for the changing height of the center of gravity?
Any help is appreciated.

 

[gleem]

Once L=Wa/x and the table is on the verge of tipping any additional load will cause the table to tip. The tipping torque of the load will become greater than the restoring torque of the weight because the perpendicular distance of the line of action of the load to the rotation point increases and the perpendicular distance of the line of action of the weight to that point decreases.

If you want to know how fast it tips then you need to modify the equation to take into account the tipping angle as the table rotates since the net torque will increase as it rotates over.

 

[william497]

Thanks for the quick reply.
I don't think you understood my question entirely. I will try to rephrase and make it clearer.
I understand that the table will tip once L>Wa/x, as you say the tipping torque is greater than the restoring torque of the weight.
I am not concerned about the tipping speed. Only the amount of load required to get the table to tip.
Lets say I have 2 tables.

Table A has a base that weighs 50kg, with a TP_to_CG distance of 200, a Ø900 top (overhang of 250) that weighs 5kg.
The equation would be L = 55 * (200/250), L=44kg

Table B has a base that weighs 5kg, with a TP_to_CG distance of 200, a Ø900 top (overhang of 250) that weighs 50kg.
The equation would be L = 55 * (200/250), L=44kg

I get the same load required to tip the table, but I know this is not accurate, because the table with the heavy top will have a higher center of gravity and will require much less load to tip the table, than the table with the with the heavy base.
My question is how does L>Wa/x take into account the changing center of gravity and give me an accurate load.

 

[gleem]

My question is how does L>Wa/x take into account the changing center of gravity and give me an accurate load.

It doesn't need to. When L< Wa/x nothing happens. When L is every so slightly > Wa/x the table will tip beginning very slowly and increasing faster as it continues to tip. There is no transition period unless there is rotational friction at the point of rotation which prevents it from starting to tip. The height of the table will then need to be taken into account.

 

[Filip Larsen]

When the table is top heavy it will tip over faster once the load exceeds the limit since the distance of the GC is further away from the pivot point, but the limit itself is the same no matter the height of CG.

 

[william497]

ok, so am I correct in adding the weight for the top and the base together to get W?
Or is W only a percentage of that, since some of the weight of the top is outside of the tipping point and would therefore be contributing to the load L?

 

[gleem]

The weight at the center of gravity includes the entire weight of the table: top, stem, and base.

 

[Baluncore]

We can ignore the vertical weight distribution, because once the table begins to tip, it becomes easier to continue to tip the table.

The analysis is only guaranteed true, if all the mass is above the fulcrum, which is true of a table standing on a flat floor, or of a mobile crane with a suspended load, on the face of the Earth.

That is the origin of the term tipping point, the load required to begin tipping, after which positive feedback continues to accelerate the process.

 

[jack action]

When the table starts to tip, this will happen:

You can see that the weight is closer (horizontally) to the vertical line over the tipping point and the load is further away (always horizontally) from the vertical line. If the shorter $x$ and the longer $a$ before it began to tip were able to tip the table, now it tips even faster.

Now if you move the CG toward the lower part of the table, you can notice that the horizontal distance from the tipping point increases. This means that the table will tip slower compared with a higher CG.

This characteristic is referred to as stability.

In the previous figure, if there are no horizontal forces, the ball should never move in both cases. But in the unstable case, if there is a slight horizontal force that appears, the ball will begin to move and won't be able to stop because the hill will create another horizontal force that will further increase the ball's acceleration. In the stable case, if there is a slight horizontal, there is an opposite horizontal force that appears when the ball begins to move, thus bringing the ball to its original position.

In both cases, the same lateral force is required to initiate the ball's motion.

 

[william497]

Thanks for the help. So, if I understand this correctly. The vertical measurement of the center of gravity has no impact on the amount of force required to start to tip the table, it only has an effect once it begins tipping.
Regardless of a heavy top/light base combination or vice versa, the amount of force required will be the same in both instances?

 

[william497]

When the table starts to tip, this will happen:

View attachment 336412​

You can see that the weight is closer (horizontally) to the vertical line over the tipping point and the load is further away (always horizontally) from the vertical line. If the shorter $x$ and the longer $a$ before it began to tip were able to tip the table, now it tips even faster.

Now if you move the CG toward the lower part of the table, you can notice that the horizontal distance from the tipping point increases. This means that the table will tip slower compared with a higher CG.

This characteristic is referred to as stability.

View attachment 336413​

In the previous figure, if there are no horizontal forces, the ball should never move in both cases. But in the unstable case, if there is a slight horizontal force that appears, the ball will begin to move and won't be able to stop because the hill will create another horizontal force that will further increase the ball's acceleration. In the stable case, if there is a slight horizontal, there is an opposite horizontal force that appears when the ball begins to move, thus bringing the ball to its original position.

In both cases, the same lateral force is required to initiate the ball's motion.

I am wondering if I am using the wrong metric to measure the table's stability (vertical load before tipping).
With the diagram adjusted to be a sideways force on the top, what would the equation look like to get the table to start to tip?

 

[Lnewqban]

I am wondering if I am using the wrong metric to measure the table's stability (vertical load before tipping).
With the diagram adjusted to be a sideways force on the top, what would the equation look like to get the table to start to tip?

Please, see:
https://www.physicsforums.com/threads/torque-before-slipping-in-a-refrigerator.1058113/#post-6975743

 

[jack action]

I am wondering if I am using the wrong metric to measure the table's stability (vertical load before tipping).
With the diagram adjusted to be a sideways force on the top, what would the equation look like to get the table to start to tip?
View attachment 337052

The equation is always the same: The sum of the moments counterclockwise must equal the sum of the moments clockwise. The moment of a force about a point (any point) is the force times the perpendicular distance between that force at the point.

So you choose a point. Let us take the pivot point. Why the pivot point? Because that is where the reaction forces will be applied and since they are directly on the point, their distances are zero, and with it, their moments about that point are also zero. It simplifies everything. In our case, the pivot point is on the left at the end of the base, so:
$$M_{ccw} = M_{cw}$$
$$L \times h = W \times a$$
Or:
$$L = \frac{a}{h}W$$
If $L$ is greater than this value, the system is NOT in equilibrium anymore and the table will start to move, i.e. tip.

 

[Nik_2213]

Humour:
Regardless of 'static' math, one (1) low-flying cat will so manage it...
/

 

[sophiecentaur]

The vertical measurement of the center of gravity has no impact on the amount of force required to start to tip the table,

Yes. But the angle at which the table can be tilted is very much affected. In practical terms, this is very very relevant. As @jack action points out, stability is the relevant factor as all vehicle designers will tell you about cornering performance. Imagine giving the table a mild side-swipe as you walk past when it's got a heavy pile of books on it. which design is safer?

 

[Nik_2213]

Having once ridden in a 2CV, I sorta kissed the ground after scrambling out of that 'Wibbly-Wobbly' horror, given its infamous aversion to bends and, especially, roundabouts. Think motor-bike +side-car combo or 'trapeze' one-design dinghy...

This stability is also an essential factor in ship design. Even a modest change of centre-of-gravity vs centre-of-buoyancy heights can dramatically change the 'ride'. Hence the concerns of 'Box Ship' loadmasters, and the designers of naval craft, who want to put sensors high, but keep c/g low for sea-worthiness. Many such war-craft have 'lightweight' upper-works to save vital tonne-metres. Upside, more stability, especially welcome for inclement weather / sea-state. Down-side, damage control...