Calculating Time Between Two Projectile Collisions

In summary, the problem involves two balls being thrown at different angles with the same initial velocity and colliding at a distance y. The vertical velocity at the collision point is unknown and the question is to find the time between when the two balls were thrown. The solution involves using the equations of motion for horizontal and vertical motion, but finding the time between the throws is difficult and may require another approach.
  • #1
sara_87
763
0

Homework Statement



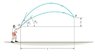
At time t1, the boy throws a ball at an angle theta1
After some time (say t2), the boy throws another ball at an angle theta2
The initial velocity for both balls is the same (say v0)
The balls collide at B, a distance of y (as shown in the attachment)
the veritcal velocity at B is unknown
The question is:
Find the time between when the 2 balls were thrown.

Homework Equations



horizontally: the velocity stays the same, the distance is x, there is no acceleration.
vertically: the acceleration is g (under free gravity)

The Attempt at a Solution



Horizontally:
first ball: x = v0cos(theta1)t1 (using the equation s = ut + 1/2 at^2)
second ball: x = vocos(theta2)t2

vertically:
first ball: y = v0sin(theta1)t1 + 1/2 g(t1)^2
second ball: y = v0sin(theta2)t2 + 1/2 g(t2)^2

I tried to make t1 the subject from the horizontal equations but after substituting them into the vertical equations, i found it difficult to make t2 the subject (if it is even possible).
so, maybe there is another approach.

Any help is very much appreciated.
Thank you.
 

Attachments

  • qn.jpg
    qn.jpg
    10.9 KB · Views: 342
Physics news on Phys.org
  • #2
I suggest posting this in the physics forum...
 

FAQ: Calculating Time Between Two Projectile Collisions

How do you calculate the velocity of a projectile after a collision?

The velocity of a projectile after a collision can be calculated using the conservation of momentum principle. This means that the total momentum before the collision is equal to the total momentum after the collision. By equating the initial and final momentum equations, the velocity of the projectile after the collision can be obtained.

What factors affect the outcome of a collision between two projectiles?

The outcome of a collision between two projectiles can be affected by several factors such as the masses of the projectiles, their velocities before the collision, and the angle at which they collide. Other factors like the elasticity of the objects and external forces can also play a role in determining the outcome of the collision.

Can the kinetic energy of a projectile change after a collision?

Yes, the kinetic energy of a projectile can change after a collision. In an elastic collision, the kinetic energy is conserved, meaning that the total kinetic energy before the collision is equal to the total kinetic energy after the collision. In an inelastic collision, some kinetic energy is lost and converted into other forms, such as heat or sound energy.

How does the angle of collision affect the final velocities of the projectiles?

The angle of collision can affect the final velocities of projectiles in different ways. If the two projectiles collide head-on, the angle of collision is 0 degrees and the final velocities will be equal. However, if the angle of collision is not 0 degrees, the final velocities will be different and can be calculated using the conservation of momentum and energy principles.

What is the difference between an elastic and inelastic collision?

An elastic collision is one in which both the momentum and kinetic energy are conserved. This means that the total momentum and kinetic energy before the collision are equal to the total momentum and kinetic energy after the collision. In contrast, an inelastic collision is one in which some kinetic energy is lost and converted into other forms, such as heat or sound energy. However, the total momentum is still conserved in an inelastic collision.

Similar threads

Timing a bouncing ping-pong ball
Replies
19
Views
2K
Velocity of the ball when it hits the ground, limits?
Replies
17
Views
3K
A ball is thrown w/initial speed vi at an angle 𝜃i with the horizontal
Replies
5
Views
814
A Interpretation of Lagrangian solution (complex numbers)
Replies
2
Views
851
Ball launched from a height of 5 meters --- Projectile motion
Replies
12
Views
488
Oblique soccer shot calculation task
2
Replies
38
Views
3K
Compare the ratio of two times t1/t2 in this vertical jump
Replies
3
Views
727
Projectile Motion 2D - Spring Launched
Replies
3
Views
2K
Ball Release and Thrown to reach ground at the same time
Replies
1
Views
2K
I If we throw a ball with initial velocity v0, is there a force?
Replies
3
Views
1K

Hot Threads

Recent Insights

Back
Top