Calculating Torque and Linear Acceleration of a Rotating Rod

[ScienceGeek24]

Homework Statement

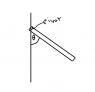
A uniform rod of mass M and length L is free to rotate about a pivot at the left end. It is released from rest in the horizontal position ( Thetha=90 degrees). What is the torque on the rod when it makes and angle (theta) with the vertical? What is the downward linear acceleration of the right end of the rod when it is first released (at Thetha=90degrees)?

Homework Equations

T=Ialpha, t=+-rFsintheta

The Attempt at a Solution

For the first part of the question i manged to solve by with -rFsin(theta) my radius was half of the length of the rod, my force was found inthe center of mass of the rod which was mg and multiply that by sin(theta) according to the formula i get -(Lmg sin(theta)/2). The second part is thepart where I'm having trouble with. I know that it has to do with t=I(alpha) since we are looking for linear acceleration. But i don't seem to know how to start up with because I no no units. Any help on this one??

 

[gneill]

What's the relationship between linear and angular acceleration?

 

[ScienceGeek24]

α = Δω / Δt for angular and a = v^2/r for tangential or centripetal. DO we need linear as of a=d*t ??

 

[gneill]

α = Δω / Δt for angular and a = v^2/r for tangential or centripetal. DO we need linear as of a=d*t ??

There is a direct relationship between linear acceleration and angular acceleration when the radius is known. If a vector r is rotating and has angular acceleration $\alpha$, then the tip of the vector has tangential (linear) acceleration $\alpha r$.

 

[ScienceGeek24]

yeah but in the problem, the radius is not known. This is confusing. you only have an angle which is 90 degrees. You don't have a radius, without that how can I calculate αr to find the tangential (linear) acceleration??

 

[ScienceGeek24]

i know that angular velocity is V^2/r but i don't have a velocity given neither. I don;t have the mass of the object so I cannot calculate the force on the object mgsin(theta).

 

[gneill]

yeah but in the problem, the radius is not known.
This is confusing. you only have an angle which is 90 degrees. You don't have a radius, without that how can I calculate αr to find the tangential (linear) acceleration??

Don't you have a symbol for the length of the rod? You're interested in finding the initial acceleration of its end, right?

 

[ScienceGeek24]

the answer to the problem is -14.7 m/s^2 ... how to reach to that problem without so many variables... this one is difficult.

 

[gneill]

i know that angular velocity is V^2/r but i don't have a velocity given neither. I don;t have the mass of the object so I cannot calculate the force on the object mgsin(theta).

No, V²/r is centripetal acceleration, which is not angular acceleration. In fact, an angular equation for centripetal acceleration is ω²r. Just thought you might like to know that

 

[ScienceGeek24]

1/12?? so are you saying that is my total length?? and i shold multply α(1/12)?? to finf linear acceleration?

 

[gneill]

1/12?? so are you saying that is my total length?? and i shold multply α(1/12)?? to finf linear acceleration?

 

[ScienceGeek24]

ROFLMAO! I don't know... i can't really come up with a set up.

 

[gneill]

If this were a linear kinematics problem and you wanted to find acceleration, the first thing you'd think of is F=MA and go about looking for the force. For angular motion, torque is the equivalent of force.

Start from the basics. What's the expression for the torque about the pivot when the rod is horizontal?

 

[ScienceGeek24]

-(Lmgsin(theta)/2?

 

[gneill]

-(Lmgsin(theta)/2?

Come on, what's θ when the rod's horizontal?

 

[ScienceGeek24]

-(Lmgsin(90)/2?

 

[gneill]

-(Lmgsin(90)/2?

Follow though! What's sin(90°)?

 

[ScienceGeek24]

sin(90) is 1

 

[gneill]

sin(90) is 1

...which makes the expression for the torque...

 

[ScienceGeek24]

-1/2Lmg

 

[ScienceGeek24]

BUt what about L and m ? we don't have any of them.

 

[gneill]

-1/2Lmg

Okay, so you've got the "force", now you need the "mass". What's the angular equivalent of mass?

 

[ScienceGeek24]

1/12ml^2?

 

[ScienceGeek24]

i think i know whare you are going with this -1/2Lmg=1/12ml^2(w)^2?

 

[ScienceGeek24]

from t=Iw^2?? so thatis why you were saying that angular velocity and tangential velocity had a relationship so my w becomes v^2/r?? but how do i cancel out the r??

 

[gneill]

1/12ml^2?

Well, I meant in general. It's the moment of inertia.

You've given the moment of inertia for a slender rod about its center. This rod is pivoted at one end. What's the moment of inertia for a slender rod pivoted about its end?

 

[gneill]

from t=Iw^2?? so thatis why you were saying that angular velocity and tangential velocity had a relationship so my w becomes v^2/r?? but how do i cancel out the r??

As I stated before, angular acceleration is NOT centripetal acceleration. V^2/r does not come into play here.

 

[ScienceGeek24]

-1/2Lmg=1/3 M L^2(w)^2 ?

 

[gneill]

i think i know whare you are going with this -1/2Lmg=1/12ml^2(w)^2?

That's the right idea, but you need the correct moment of inertia, and you are looking for the angular acceleration ($\alpha$).

 

[ScienceGeek24]

so is just solving for w??

 

[ScienceGeek24]

-1/2Lmg=1/3 M L^2(alpha) ? is this right?

 

[gneill]

-1/2Lmg=1/3 M L^2(w)^2 ?

There's no w^2. Newton's second law for rotation is $\tau = I \alpha$

 

[ScienceGeek24]

now, how do i cancel the Ls? one has L and the other one has L^2?? even if i manage to cancel them out i don't get the right answer.

 

[gneill]

now, how do i cancel the Ls? one has L and the other one has L^2?? even if i manage to cancel them out i don't get the right answer.

You're not done yet. Solve for $\alpha$. What expression do you get?

 

[ScienceGeek24]

α=-1/2g-1/3L