Calculating torque for precessing gyroscope

[Cleonis]

I'm presenting a computation. I'm posting here to ask if anyone spots an error either in the reasoning or in the math.

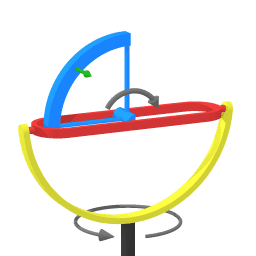
The image shows a gimbal mounted spinning gyroscope wheel.
The brown cilinder represents a weight, exerting a torque.

Naming convention:
Spinning of the wheel: rolling
rotation of the red housing: pitching
rotation of the yellow housing: swiveling

For computation I visualize the motion quadrant by quadrant.

All parts of that quadrant are moving towards the swivel axis.
The wheel is swiveling at a constant rate. Whenever circumnavigating mass is pulled closer to the central axis of rotation it tends to pull ahead of the circumnavigating motion. The green arrow represents that tendency. Conversely, when mass moves away from an axis of rotation it tends to lag behind.

Combined over all four quadrants the wheel will have a strong tendency to pitch. If the gimbal mounted gyroscope wheel is free to pitch then the rolling axis will become aligned with the swivel axis. What I want to calculate: given a particular swivel rate and rolling rate, how much torque is required to prevent that pitching?
This calculation is for the simplest case: a thin-walled cylinder with radius R.

Method: integration along the circumference of the wheel.
$$\int\limits_{0}^{2\pi} f(\theta) \, d\theta$$

Naming:
Rolling rate: $$\omega_r$$
Swiveling rate: $$\omega_s$$

Mass per unit of arc : M/2*pi
Velocity component towards/away from central axis: $$v_r = \omega_r R \sin(\theta)$$
Distance to pitch axis: $$\sin(\theta) R$$
Tendency to pull ahead/lag behind overall swiveling: $$F = 2 m \omega_s v_r$$

This gives the following integral:
$$\int\limits_{0}^{2\pi} \big( 2 \frac{M}{2\pi} \omega_s \omega_r R \sin(\theta) \big) \big( \sin(\theta) R \big) \, d\theta$$

Rearranging:
$$\int\limits_{0}^{2\pi} \frac{M}{\pi} \omega_s \omega_r R^2 \sin^2(\theta) \, d\theta$$

sin²(x) is substituted with (1/2 - 1/2cos(2x))

$$\int\limits_{0}^{2\pi} \sin^2(\theta) \, d\theta = \int\limits_{0}^{2\pi} \big( \tfrac{1}{2} - \tfrac{1}{2}cos(2\theta) \big) \, d\theta = \pi$$

The question was: given a particular swivel rate and rolling rate, how much torque is required to prevent pitching? This calculation yields:

$$M \omega_s \omega_r R^2$$

I haven't yet compared this result with the usual calculation that is presented in physics textbooks.

 

[Cleonis]

[...] given a particular swivel rate and rolling rate, how much torque is required to prevent pitching? This calculation yields:

$$M \omega_s \omega_r R^2$$

I haven't yet compared this result with the usual calculation that is presented in physics textbooks.

Rearranging (and using the greek letter 'tau' for 'torque'):

$$\tau = \omega_s \omega_r M R^2$$

The angular momentum of the rotor is $$\omega_r M R^2$$

$$\tau = \omega_s L_r$$

Gratifyingly, this matches the expression given in textbooks, where it is usually derived in the following form:

$$\omega_s = \frac {\tau}{L_r}$$

What I find interesting is that the calculation strategy of integrating the rotation-effect around the circle did not use the angular momentum around the rolling axis, but it did arrive at an expression that contains that angular momentum.