Calculating Torque on this Square

[Addie M]

Homework Statement

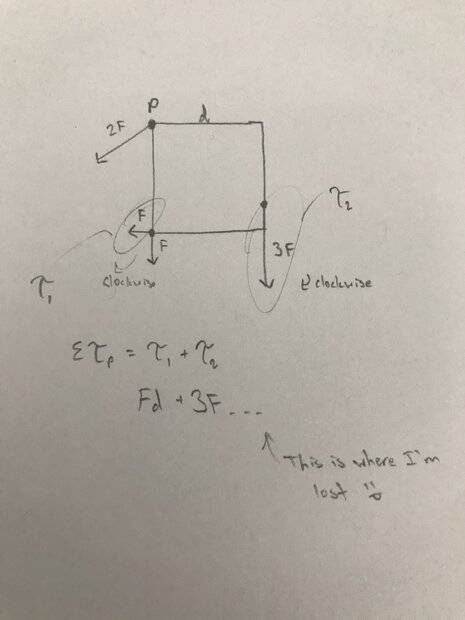
Find the net torque of the square in terms of F and d

Relevant Equations

T=r×F=rFsin(θ)

So I started by just figuring out what forces are going to have torque. I know the one heading straight down from the pivot won’t have any and the one going at an angle from the pivot won’t be included in the net torque since it’s at the pivot. The rest of the forces have torque and they are both clockwise (going the same direction). I can get the torque for the F on the bottom left (it’s just Fd), but I can’t figure out how to find the torque for the 3F since it’s starting point isn’t as the corner. How would I find that? And how would I represent it in my formula to find net torque?

 

[TSny]

Besides the equation $\tau = r F \sin \theta$, have you learned any equivalent ways to express torque? In particular, have you covered the concepts of "line of action of a force" and "lever arm" of a force? Another name for "lever arm" is "moment arm".

 

[Addie M]

Well I know that the angle is found from the force and lever arm, I’ve used that for some more real work esque problems with ladders and diving boards. I don’t see how I could use that here with the radius since I can’t even find that.

 

[Lnewqban]

Please, see:
http://hyperphysics.phy-astr.gsu.edu/hbase/torq2.html

 

[Addie M]

Please, see:
http://hyperphysics.phy-astr.gsu.edu/hbase/torq2.html

What would I enter in for radius though since I don’t have any actual measurements only variables?

 

[Lnewqban]

What would I enter in for radius though since I don’t have any actual measurements only variables?

Copied from:
https://engcourses-uofa.ca/books/statics/forces-and-moments/moments/#principle-of-transmissibility4

"The location of the point at which the force is acting does not affect its moment about a given point as long as the point is selected on the line of action of the force. This fact is referred to as the principle of transmissibility stating that sliding a force along its line of action does not change its moment about a given point. By this principle, a force vector is designated as a sliding vector."

 

[haruspex]

Homework Statement: Find the net torque of the square in terms of F and d

First, that is an incomplete question. Except in the case of a 'pure' torque (i.e. where there is no net force) a torque is only meaningful in respect of a defined axis. If you calculate the torque about one corner of the square you will get a different result depending on the corner you choose, and different again from that about the middle of the square.

Were you told to use the bottom top left corner? If not, it is safest to assume it means the middle of the square.

For torques, the exact point of application of a force does not matter. What matters is the "line of action". I.e. you can pick any point along its line as the point of application.
There are several ways to calculate a torque. See https://www.physicsforums.com/insights/frequently-made-errors-mechanics-moments/. In each, as you can see, displacing the point of application along the line of action makes no difference.

 

[Addie M]

First, that is an incomplete question. Except in the case of a 'pure' torque (i.e. where there is no net force) a torque is only meaningful in respect of a defined axis. If you calculate the torque about one corner of the square you will get a different result depending on the corner you choose, and different again from that about the middle of the square.

Were you told to use the bottom left corner? If not, it is safest to assume it means the middle of the square.

For torques, the exact point of application of a force does not matter. What matters is the "line of action". I.e. you can pick any point along its line as the point of application.
There are several ways to calculate a torque. See https://www.physicsforums.com/insights/frequently-made-errors-mechanics-moments/. In each, as you can see, displacing the point of application along the line of action makes no difference.

Yes, I’m trying to find the net torque on that exact pivot point. Could you also explain sliding vectors to me a little more. From what I understand, I can just move the entire pivot point down and the radius for T2 would be d, but then I would run into the same problem I did originally with T1 where I can’t find the radius. Or am I getting that totally wrong?

 

[TSny]

Were you told to use the bottom left corner? If not, it is safest to assume it means the middle of the square.

The top left corner is marked “p”, presumably for “pivot point”. Apparently, this is the point about which the torques are taken. But, yes, the problem statement could have been clearer about this.

 

[Addie M]

Copied from:
https://engcourses-uofa.ca/books/statics/forces-and-moments/moments/#principle-of-transmissibility4

"The location of the point at which the force is acting does not affect its moment about a given point as long as the point is selected on the line of action of the force. This fact is referred to as the principle of transmissibility stating that sliding a force along its line of action does not change its moment about a given point. By this principle, a force vector is designated as a sliding vector."

We haven’t discussed anything about sliding vectors or lines of action yet in class, so I’m really lost on how I would use that in order to solve this problem and find the radius of T2 in terms of d.

 

[haruspex]

From what I understand, I can just move the entire pivot point down

No, don’t move the pivot point.
As I wrote, there are several ways to calculate a torque given a force and a pivot. One is to multiply the magnitude of the force by the perpendicular distance from the pivot to the line of the force. E.g. for the 3F about P, that's 3Fd (clockwise). So where the 3F is applied along its line does not matter.

 

[Addie M]

No, don’t move the pivot point.
As I wrote, there are several ways to calculate a torque given a force and a pivot. One is to multiply the magnitude of the force by the perpendicular distance from the pivot to the line of the force. E.g. for the 3F about P, that's 3Fd (clockwise). So where the 3F is applied along its line does not matter.

So would that perpendicular line be a diagonal line from the pivot point to the point where the 3F starts or a horizontal one from the pivot point to the side where the 3F is? I assume it’s the first one but I have no idea how to find the value of the diagonal line (radius) since I only have the value on one side (the d on top). I thought about putting d-x on the right side of the square and then use pythagorean theorem to find the hypotenuse (here that would be the diagonal line or radius I drew from the pivot to the point where 3F starts) but I can’t figure out how to calculate that. Am I going at this the right way or should I be doing something different?

 

[erobz]

So would that perpendicular line be a diagonal line from the pivot point to the point where the 3F starts or a horizontal one from the pivot point to the side where the 3F is? I assume it’s the first one but I have no idea how to find the value of the diagonal line (radius) since I only have the value on one side (the d on top). I thought about putting d-x on the right side of the square and then use pythagorean theorem to find the hypotenuse (here that would be the diagonal line or radius I drew from the pivot to the point where 3F starts) but I can’t figure out how to calculate that. Am I going at this the right way or should I be doing something different?

It's either the force times the perpendicular distance to $P$ or the distance to $P$ times the component of the force that is perpendicular to that distance.

Try solving it both ways. First, you are on the right track for the way that requires more work, but none the less if you correctly push through you will arrive at the same result for both cases. Having the result from that method will illuminate the simplest method for this problem.

 

[Addie M]

It's either the force times the perpendicular distance to $P$ or the distance to $P$ times the component of the force that is perpendicular to that distance.

Try solving it both ways. You are on the right track for the way that requires more work, but none the less if you correctly push through you will arrive at the same result.

For either method wouldn’t I need the value for the radius (diagonal line from pivot to the point where 3F starts)? The problem I’m having is I still have no idea how to get that radius value. Like I said, I put in d-x for the side I didn’t know, but the value I got for the radius is a mess and I’m doubting if it’s even right since the question is making it seem that the answer is going to be simple.

 

[erobz]

For either method wouldn’t I need the value for the radius (diagonal line from pivot to the point where 3F starts)? The problem I’m having is I still have no idea how to get that radius value. Like I said, I put in d-x for the side I didn’t know, but the value I got for the radius is a mess and I’m doubting if it’s even right since the question is making it seem that the answer is going to be simple.

This is what you have done, what is the distance $l$? Hint don't get fancy and expand it all out under the root, just give me $l$ by applying Pythagorean Theorem.

This is the method that finds the distance between the point of application of the force to $P$, and then we will find the component of that force that is perpendicular to $l$, with some basic trig. Does that sound ok?

Also, we use Latex here to format math equations, not hard to learn. see LaTeX Guide

 

[Addie M]

View attachment 332371

This is what you have done, what is the distance $l$?

Also, we use Latex here to format math equations, not hard to learn see LaTeX Guide

Well thats just the sqrt of d^2 + (d-x)^2 which is a messy value. But wouldn’t whatever that value is multiplied by sin of our unknown angle just be d?

 

[erobz]

Well thats just the sqrt of d^2 + (d-x)^2 which is a messy value. But wouldn’t whatever that value is multiplied by sin of our unknown angle just be d?

Maybe you are on to something? Do you want to continue on? Have you had a Eureka moment?

 

[Addie M]

Maybe you are on to something? Do you want to continue on, or do you to examine the other method?

I think I might have been overthinking this way too much. Is the answer just 4Fd? Since the torque of T1 is Fd , T2 is 3Fd, and they are rotating in the same direction?

 

[erobz]

Just to be clear, you were going to find the red component, $3F \sin \theta = 3F \frac{d}{l}$, and then you were going to multiply by $l$ to get the torque leaving you with $3F d$, which is found by inspection using the distance that is perpendicular from $F$ to $P$ ( i.e. $d$ ) times the force $3F$.

 

[Addie M]

View attachment 332372

Just to be clear, you were going to find the red component, $3F \sin \theta = 3F \frac{d}{l}$, and then you were going to multiply by $l$ to get the torque leaving you with $3F d$, which is found by inspection using the distance that is perpendicular from $F$ to $P$ ( i.e. $d$ ) times the force $3F$.

That makes a lot more sense. Thanks so much!

 

[Lnewqban]

We haven’t discussed anything about sliding vectors or lines of action yet in class, so I’m really lost on how I would use that in order to solve this problem and find the radius of T2 in terms of d.

Since you have a square, you have four sides of length d.
Just to test the idea that has been discussed above, relocate the point of application of the force 3F to the top corner first, and then to the bottom corner.
In the first case, the lever of the force will be d.
That gives us a value of τ2 equal to 3Fd.

In the second case, the lever of the force will be the diagonal line of the square, joining the pivot P and our second imaginary point of application (d√2).
However, the force inducing τ2 in this case is the component of 3F that is perpendicular to that lever.
Because trigonometry, the value of that perpendicular component is 3F/√2.
As you can see, that configuration also gives us a value of τ2 equal to 3Fd.

Therefore, the actual point of application of 3F in our diagram does not make a difference in the value of τ2, as long as 3F is applied along the edge of the square (same line of force application).