- #1
paulmdrdo
- 89
- 2
I wonder if there's a physics person here who could help me solve this problem.
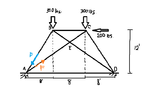
the loads applied to the truss shown in the figure cause reactions shown at A & D. A free body diagram of hinge A forms concurrent force system shown enclosed at A. Determine the magnitude of forces P & F directed respectively along bars AB & AE that maintain equilibrium of this system.
the loads applied to the truss shown in the figure cause reactions shown at A & D. A free body diagram of hinge A forms concurrent force system shown enclosed at A. Determine the magnitude of forces P & F directed respectively along bars AB & AE that maintain equilibrium of this system.