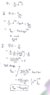Calculating total charge when the electric field is given

[Saptarshi Sarkar]

Homework Statement

Calculate the total charge of an unknown charge distribution for which the electric field is E=q/r^2 e^(-4r) r ̂

Relevant Equations

E.A = q/ε0
∇·E = ρ/ε0

I first tried to use the Gauss' law equation E.A = q/ε0 to find the total charge enclosed. The answer came out to be q(enclosed) = 4πqε0e^(-4r). So for r approaching infinity, q(enclosed) approached 0.

Next, I tried the equation ∇·E = ρ/ε0, calculated rho to be -4qε0e^(-4r)/r^2 and total charge to be -4πqε0.

Why are the answers different although both are derived from Gauss' law? What did I do wrong?

 

[Orodruin]

Your computation for the divergence of the electric field is only valid for $r > 0$. This means that you will miss the contribution from the point charge at the origin.

 

[Paul Colby]

Another thing you might think about is how the given electric field behaves as $r$ gets really big. Compare this to what the field of any point charge, $q_o$, behaves for large $r$. What does $q_o$ have to equal so that these distant fields are the same.

 

[Saptarshi Sarkar]

Another thing you might think about is how the given electric field behaves as $r$ gets really big. Compare this to what the field of any point charge, $q_o$, behaves for large $r$. What does $q_o$ have to equal so that these distant fields are the same.

For both the cases, the electric field approaches 0 as r approaches large numbers. Only conclusion I can draw from this is that the given electric field falls to 0 faster due to the exponential term.

 

[Saptarshi Sarkar]

Your computation for the divergence of the electric field is only valid for $r > 0$. This means that you will miss the contribution from the point charge at the origin.

I am not sure I am able to understand. How do I know that there is a charge at the centre and how should I calculate it?

 

[Orodruin]

If you compute the divergence with a method valid at $r = 0$, you will find that, apart from your result, there is a delta function at the origin.

Alternatively, you can check this by taking the flux through a sphere with $r \to 0$, which will yield a non-zero result, indicating that there is a point charge at the origin.

 

[Saptarshi Sarkar]

If you compute the divergence with a method valid at $r = 0$, you will find that, apart from your result, there is a delta function at the origin.

Alternatively, you can check this by taking the flux through a sphere with $r \to 0$, which will yield a non-zero result, indicating that there is a point charge at the origin.

Is this what you are saying?

https://physics.stackexchange.com/questions/488220/divergence-of-frac-hat-bf-rr2-what-is-the-paradox

 

[Orodruin]

Yes.