Calculating Voltage Across Capacitor: EMF and Internal Resistance Question"

[coffeem]

Homework Statement

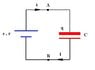
At time t=0, a cell of EMF E and internal resistance r is connected to the capacitor of Capacitance C.

i) Derive an expression for the voltage across the capacitor at subsequent times.

ii) If the capacitance is 5000uF and the voltage across the capacitor reaches 73 V at a time 10ms after connection, before tending towards a steady value of 150V, what are the values of the cell's EMF and internal resistance?

Homework Equations

E = V - IR?

The Attempt at a Solution

I am unsure about part i. I know for the second part i will have to solve a simultaneous equation... However I can't get part i.

Any advice would be greatly appreciated! Thanks

 

[hikaru1221]

You can consider the cell with internal resistance as a perfect cell, which has no internal resistance, in series with a resistor whose resistance = r. Then what do you have for voltage u, charge q, and current i?

 

[coffeem]

Umm I really don't know.

V = e - Ir

can you give me some more adivce. I have the answer but have no idea how the question askerer has got there! thanks

 

[hikaru1221]

In these kinds of questions, we must be very careful in considering v, i and q, as it will affect the signs.

Consider the circuit like in the picture. Choose q as the charge of the upper plate. Choose the (+) direction of current i as in the picture. Consider the potential difference between 2 points A and B:
_ For the battery: $$V_{AB}=e-ir$$
_ For the capacitor: $$V_{AB}=q/C$$
_ Because the current i is "coming into" the upper plate: $$i=dq/dt$$
From here, you can solve for $$V_{AB}$$. Note that if you choose q and i the way around, or consider $$V_{BA}$$ instead, the sign corresponding to each in those equations will change.