- 1,753
- 143
Find the volume of the solid obtained by rotating the region bounded by the given curves about the specified line.
y=1/x, x=1, x=2, y=0; about the x-axis
About halfway down, I diverge into two methods. The one on the left I use the method from FrogPad's post in my other thread (or at least my effort to understand the method he describes, btw, thank you). But it gives me 3pi/2. The one on the right gives me the same answer as the back of the book, pi/2. Maybe neither is right, and I coincidentlly got the right answer using the method on the right
Also, am I using the right symbols, etc.?
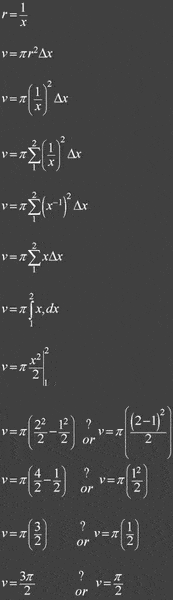
y=1/x, x=1, x=2, y=0; about the x-axis
About halfway down, I diverge into two methods. The one on the left I use the method from FrogPad's post in my other thread (or at least my effort to understand the method he describes, btw, thank you). But it gives me 3pi/2. The one on the right gives me the same answer as the back of the book, pi/2. Maybe neither is right, and I coincidentlly got the right answer using the method on the right

Also, am I using the right symbols, etc.?