Calculating Water Velocity Using Bernoulli's Equation

In summary, the velocity of water exiting the hole in the diagram can be found using the Bernoulli equation. The kinematic equations can be used to determine the time for the water to hit the ground, the value of H, the horizontal distance of flight, and the acceleration of gravity. Alternatively, conservation laws can also be applied, though momentum may not be conserved in the vertical direction due to the force of gravity.
  • #1
Gamma
357
11
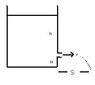
The velocity of the water that comes out of the opening in the attached diagram can be found using Bernoulli equation, as

v = sqrt (2gh)

Once the water exits the hole, I am not sure how to answer questions like the following: Can I use conservation of energy and momentum. Also can I use the equations in kinematics (ie. S = ut + 1/2 a t^2, v=u+at,...)

1. Time for the water to hit the ground,
2. What is the value of H
3. What is the horizontal distance of flight of water
4. What is the acceleration ( acce. of gravity??)


Thanks a lot.

Gamma.
 

Attachments

  • waterflow.JPG
    waterflow.JPG
    2.5 KB · Views: 418
Last edited:
Physics news on Phys.org
  • #2
Usually the kinematic equations are all you need assuming you know the initial geometry of the set up. I see no picture, so I can't tell.
 
  • #3
Yes the pic did not show up. It is there now. Sorry.
 
  • #4
How about conservation of energy and momentum? I can cosider a mass of water that exits the hole per unit time as 'm' and write the conservation lows. Is seems ok to do that.

edit: May be momentum is not conserved in the vertical direction due to the force of gravity.?
 
Last edited:
  • #5
You could use conservation laws also, I presume
 

FAQ: Calculating Water Velocity Using Bernoulli's Equation

What is Bernoulli's equation and how is it used to calculate water velocity?

Bernoulli's equation is a fundamental equation in fluid dynamics that relates the pressure, velocity, and height of a fluid. It is used to calculate water velocity by equating the total energy at one point in a fluid system to the total energy at another point, taking into account the changes in pressure and height between the two points.

What are the assumptions made when using Bernoulli's equation for calculating water velocity?

Some of the key assumptions made when using Bernoulli's equation include: the fluid is incompressible, the flow is steady, the fluid is non-viscous, and there is no energy loss due to friction or turbulence. These assumptions may not hold true in all cases, so it is important to carefully consider their validity before using the equation.

What units should be used when plugging values into Bernoulli's equation for water velocity calculations?

Bernoulli's equation requires consistent units, so it is important to use the same units for all variables. Common units for water velocity calculations include meters per second (m/s), feet per second (ft/s), and miles per hour (mph). It is important to check and convert all units before plugging values into the equation.

How accurate are water velocity calculations using Bernoulli's equation?

The accuracy of water velocity calculations using Bernoulli's equation depends on the accuracy of the measurements and the validity of the assumptions made. In ideal conditions, the equation can provide accurate results, but in real-world situations, there may be some error due to factors such as energy losses and turbulence.

Can Bernoulli's equation be used for all types of fluid flow?

Bernoulli's equation is applicable to many types of fluid flow, including both laminar and turbulent flow. However, it may not accurately describe certain types of flow, such as highly compressible or viscous fluids. It is important to consider the nature of the fluid flow and the validity of the assumptions before using the equation.

Similar threads

How to calculate the velocity of water streaming into the boat?
Replies
19
Views
601
Bernoulli’s Equation for plugging finger into dike under water
Replies
4
Views
1K
Bernoulli’s Equation and External Forces
Replies
4
Views
1K
What's the pressure long before the fluid exits a pipe?
Replies
13
Views
642
Bernoulli equation for calculation of water flow
Replies
30
Views
2K
Bernoulli equation / fluid flow / finding height
Replies
6
Views
2K
Formula derivation connecting vertical water flowrate & horizontal distance moved by a suspended sphere
6
Replies
207
Views
7K
Problem related to the Bernoulli Equation
Replies
16
Views
2K
Bernoulli's equation and water exit speed from tank opening
Replies
29
Views
4K
Bernoulli equation (watering can)
Replies
2
Views
1K

Hot Threads

Recent Insights

Back
Top