Aurelius120
- 269
- 24
- Homework Statement
- I came across this question in my textbook
- Relevant Equations
- Power=Work/Time=Force×Velocity
I tried to solve it by integrating force from 0 to L
dF=dm.g
where dm=λdx
And then I multiplied it with velocity to get power because velocity is constant
∫(vdF)=v ∫(dF)
But the book used integration to find work done and divided it by time for power
My answer was λlgv(Option B)
Giving (Option C) as answer
Where am I wrong?
Thanks for the help
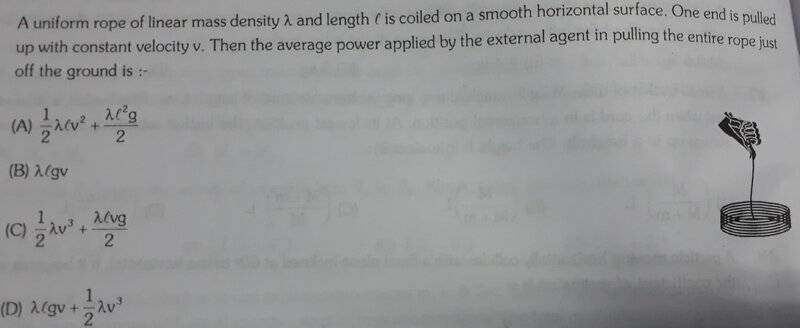
dF=dm.g
where dm=λdx
And then I multiplied it with velocity to get power because velocity is constant
∫(vdF)=v ∫(dF)
But the book used integration to find work done and divided it by time for power
My answer was λlgv(Option B)
Giving (Option C) as answer
Where am I wrong?
Thanks for the help
