Calculation about dioide with ideal diode model method

In summary, the problem is to find the current and potential in a circuit using the ideal diode model method, assuming no voltage drop and resistance within the diode. The equations used are simple Ohm's Law. The attempt at a solution involves assuming diode 2 is open and calculating the equivalent resistance of the circuit. Nodal analysis may be helpful. If the diodes are ideal, they will act as shorts when forward biased. The graph of an ideal diode is shown for reference. A new problem is then introduced, asking for the current and potential in a given circuit.
  • #1
adrian116
43
0

Homework Statement



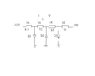
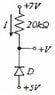
This problem is to find the I and V by ideal diode model method (assume there is no voltage drop and resistance within the diode)

Homework Equations



Just simple Ohm's Law equation

The Attempt at a Solution



First i assume the diode 2 is open, but i don't know how to calculate the equivalent resistance of the circuit? is that just all in series or R4+R2//R3+R1?
 

Attachments

  • 未命名.JPG
    未命名.JPG
    8.2 KB · Views: 689
Last edited:
Physics news on Phys.org
  • #2
I'm not sure what the V is referring to - remember the voltage is the difference in electric potential between TWO points, over an element.

Nodal analysis might be a good start.
 
  • #3
If the diode is ideal i.e. has no voltage drop across it then the diodes are effectively shorts if they are forward biased. Based on this information, redraw the circuit and work from there.
 
  • #5
new problem

The problem is:
Find I current and potential V for this circuit!
 

Attachments

  • untitled.JPG
    untitled.JPG
    5 KB · Views: 486

FAQ: Calculation about dioide with ideal diode model method

How do you calculate the forward voltage drop of a diode using the ideal diode model method?

To calculate the forward voltage drop of a diode using the ideal diode model method, you need to know the diode's characteristic parameters such as its forward current and voltage. Then, you can use the equation V = Vd - I x Rd, where Vd is the diode's forward voltage and Rd is the diode's dynamic resistance. This equation can be derived from the ideal diode model, which assumes that the diode's forward voltage remains constant regardless of the current passing through it.

What is the ideal diode model and how is it used in calculations?

The ideal diode model is a simplification of the behavior of a real diode that assumes the diode has an instantaneous and constant forward voltage drop. This model is used in calculations to simplify the analysis of circuits containing diodes, as it allows for easier and more accurate predictions of the diode's behavior. However, it should be noted that this model is not completely accurate and may not apply in all cases.

Can the ideal diode model be used for both forward and reverse bias calculations?

No, the ideal diode model is only applicable for forward bias calculations. This is because it assumes that the diode's forward voltage remains constant regardless of the current passing through it. In reverse bias, the diode's behavior is more complex and cannot be accurately modeled using the ideal diode model.

Are there any limitations to using the ideal diode model method for diode calculations?

Yes, there are some limitations to using the ideal diode model for diode calculations. This model assumes that the diode has an instantaneous and constant forward voltage drop, which is not always the case in real diodes. It also does not take into account factors such as temperature and manufacturing variations, which can affect the diode's behavior. Therefore, the ideal diode model should be used with caution and its results should be verified with real-world measurements.

How does the ideal diode model method differ from other diode calculation methods?

The ideal diode model method differs from other diode calculation methods in that it simplifies the analysis of diode circuits by assuming a constant and instantaneous forward voltage drop. Other methods, such as the piecewise-linear model or the Shockley diode equation, take into account more factors and provide a more accurate representation of the diode's behavior. However, these methods may be more complex and time-consuming to use in calculations.

Similar threads

Engineering Calculating Voltage Drop Across Non-Ideal Diodes
Replies
20
Views
4K
Engineering Calculating the voltage at a certain Resistor
Replies
3
Views
1K
Engineering Calculating Equilibrium Points in OVA-Opamp Circuit with Ideal Diodes
Replies
2
Views
899
Using Ideal and Constant Voltage Drop Models
Replies
8
Views
2K
Calculating Q points for diodes
Replies
5
Views
5K
How do I calculate the voltage of a diode in a simple electronics circuit?
Replies
9
Views
1K
Engineering What is the output voltage of this ideal diode circuit?
Replies
19
Views
4K
Solving for Zener Diode Voltage
2
Replies
45
Views
8K
Engineering Calculating Diode Current in R-V Circuit w/ Sinusoidal Input
Replies
10
Views
3K
How to find the equivalent resistance of this electric circuit?
Replies
5
Views
3K

Hot Threads

Recent Insights

Back
Top