Calculation of orbital velocity -- Geometrical solution

[sha1000]

Hello,

I would like to calculate the orbital velocity using the geometrical way of reasoning. But I have a hard time to understand and apply some basics into my calculations.

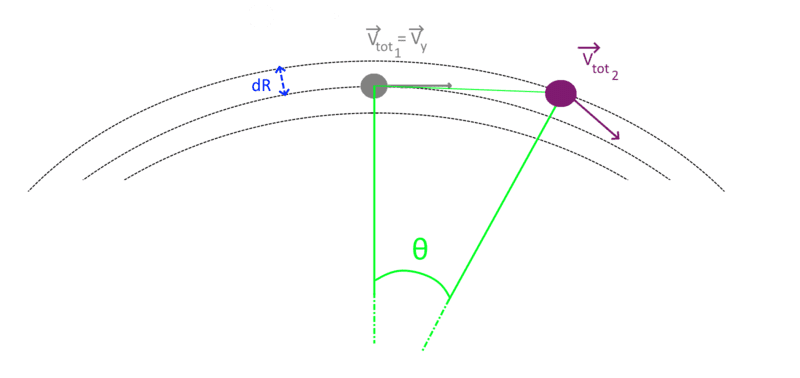
The reasoning is pretty simple. After some time: dt ,the particle travels the distance: V_tot1 * dt = R*sinθ (see the attached image). In order to stay on orbit the velocity of the particle must change accordingly, by conserving the absolute value of the velocity and changing the velocity vector by θ.

Here is the problem that bothers me. Since the initial velocity V_tot1 = V_y is perpendicular to the center of the gravitational field, after time dt the orbital radius will increase from R to R+dR (see the attached image). In this case, it means that in order to stay on the orbit; the velocity V_tot2 must be different from V_tot1. Thus, it seems to me that this problem becomes more complicated.

- Does this reasoning make any sense?
- Are there any mistakes?
- Could you please guide me into solving this calculation. it's really important for me.

Sorry for my English.

 

[Dale]

It looks like you are assuming strictly circular orbits. Is that correct? If so then the orbital velocity is just the magnitude of the initial velocity times a unit vector tangent to the circle at each point. That is fully geometrical.

What you have here is not actually a geometrical approach, but rather a numerical method called Euler's method which is known to fail for this sort of computation for the reason that you have found. If you want a better numerical result then you will need to use a better method. You may look into Hamiltonian methods, but even a standard Runge Kutta approach will be better than Euler's method.

 

[PeroK]

There's a 3blue1brown video on Feynman's lost lecture that presents a geometric solution for elliptical orbits. It's on YouTube.

 

[kuruman]

Since the initial velocity Vtot1 = Vy is perpendicular to the center of the gravitational field, after time dt the orbital radius will increase from R to R+dR

This statement is self-contradictory. For the radius to increase, you need a radial component of the velocity. If the velocity is perpendicular to the radius, there is no such component. Think of a mass swirled in a circle at the end of a string.

 

[sha1000]

It looks like you are assuming strictly circular orbits. Is that correct? If so then the orbital velocity is just the magnitude of the initial velocity times a unit vector tangent to the circle at each point. That is fully geometrical.

What you have here is not actually a geometrical approach, but rather a numerical method called Euler's method which is known to fail for this sort of computation for the reason that you have found. If you want a better numerical result then you will need to use a better method. You may look into Hamiltonian methods, but even a standard Runge Kutta approach will be better than Euler's method.

Hi Dale,

Thank you for your response. You are right I'm interested in circular orbits only.

Ok, at least I know that what I'm trying to do is a numerical method and not geometrical. I'm really surprised that there is no easy solution for it. I'll try to look into the Runge Kutta approach and see what I can get.

Can it be that the assumption V₁ = V_y is perpendicular to the radius at t=0 is false? Maybe at t=0 the angle between the velocity vector and the radius is already < 90 degrees?

 

[sha1000]

This statement is self-contradictory. For the radius to increase, you need a radial component of the velocity. If the velocity is perpendicular to the radius, there is no such component. Think of a mass swirled in a circle at the end of a string.

What I'm trying to say:
if at t=0 the velocity vector is perpendicular to the radius the particle will travel in strait line (in y direction) during dt, this implies that the position of the particle shifts to R + dR.

In order to stay on the orbit R, the initial velocity vector can not be perpendicular to the radius. At least this is what I'm thinking, maybe I'm wrong. This is why I need help with this question.

 

[PeroK]

What I'm trying to say:
if at t=0 the velocity vector is perpendicular to the radius the particle will travel in strait line (in y direction) during dt, this implies that the position of the particle shifts to R + dR.

In order to stay on the orbit R, the initial velocity vector can not be perpendicular to the radius. At least this is what I'm thinking, maybe I'm wrong. This is why I need help with this question.

That's a common mistake. A velocity vector is mathematically defined at a single point. $dt$ is the limit of $\Delta t$, as $\Delta t \rightarrow 0$.

If you use a small $\Delta t$, then you model the orbit as a polygon with many sides.

Otherwise, you model the orbit using calculus, which gives a circle.

 

[Dale]

Can it be that the assumption V1 = Vy is perpendicular to the radius at t=0 is false? Maybe at t=0 the angle between the velocity vector and the radius is already < 90 degrees?

No, that assumption is correct. The issue is that the velocity is the derivative of position, and your drawing represents a discrete time approximation to the derivative, not the derivative itself. It is this approximation which is bad and the Runge Kutta method or the Hamiltonian methods will give a better discrete approximation.

 

[Ibix]

The issue is that the velocity is the derivative of position

To expand on this, @sha1000, consider the case where the particle is at $(x,y)=(0,R)$ with velocity $(v,0)$. Your velocity updates to $(v,-g\delta t)$ and your position to $(v\delta t,R-g(\delta t)^2)$, where $g$ is the local acceleration due to gravity and $\delta t$ is the time step size. Note that your velocity no longer has magnitude $v$ and the dot product of velocity and position is $v^2\delta t-Rg\delta t+g^2(\delta t)^3=\frac{v^4}{R^2}(\delta t)^3$, where we have used that $g=v^2/R$ for a circular orbit, so velocity is no longer perpendicular to position - your orbit is no longer circular. The error is small if $\delta t$ is much less than the orbital period, but it's there and it grows.

As Dale says, you need a better integrator.

 

[sha1000]

To expand on this, @sha1000, consider the case where the particle is at $(x,y)=(0,R)$ with velocity $(v,0)$. Your velocity updates to $(v,-g\delta t)$ and your position to $(v\delta t,R-g(\delta t)^2)$, where $g$ is the local acceleration due to gravity and $\delta t$ is the time step size. Note that your velocity no longer has magnitude $v$ and the dot product of velocity and position is $v^2\delta t-Rg\delta t+g^2(\delta t)^3=\frac{v^4}{R^2}(\delta t)^3$, where we have used that $g=v^2/R$ for a circular orbit, so velocity is no longer perpendicular to position - your orbit is no longer circular. The error is small if $\delta t$ is much less than the orbital period, but it's there and it grows.

As Dale says, you need a better integrator.

Thanks to both of you.

But I have a question concerning your statement that velocity updates from (v,0) to (v, -gdt).
I'm not so sure about it, since in this case V_tot increases after dt while the particle passes from R to (R+dR). This costs energy and normally the V_tot should decrease.

Can it be that the Y component decreases while the X component gets higher;
so we go from (V_y,0) to (V_y - Adt, -gdt).

So when particle makes a quarter of circle
-> V_y= 0 and Vx = -V_{y_initial}

 

[Dale]

But I have a question concerning your statement that velocity updates from (v,0) to (v, -gdt).

That is simply referring to the Euler's method. In Euler's method you do:
$$\vec v_{n+1}= \vec v_n + \vec a(\vec r_n) \Delta t$$
$$\vec r_{n+1}=\vec r_n + \vec v_n \Delta t$$
$$\vec a(\vec r)=\frac{GM \vec r}{r^3}$$

So at $n=0$ you have $\vec v_{1}= \vec v_0 + \vec a(\vec r_0) \Delta t = (v,0) + (0,-g) \Delta t = (v,-g \Delta t)$

I would recommend instead something like the Verlet method which is one of the Hamiltonian or symplectic methods.

$$\vec r_1 = \vec r_0 + \vec v_0 \Delta t + \frac{1}{2} \vec a(\vec r_0) \Delta t^2$$
$$\vec r_{n+1} = 2 \vec r_n - \vec r_{n-1} + \vec a(\vec r_n) \Delta t^2$$

 

[Dale]

Just for demonstration I implemented the two above methods. I used $G=M=1$ with $r_0=(1,0)$ and $v_0=(0,1)$. I used $\Delta t = 0.1$ and simulated from $t=0$ to $t=10$. That $\Delta t$ is rather coarse, but shows the point well. I plotted the $x$ and $y$ components of $r(t)$

The ideal curves are

When I use Euler's method the approximate numerical curve is

You can easily see that this deviates strongly from the ideal curve, and gets pretty bad pretty quickly. This is why Euler's method is generally a poor method to use for all but the most trivial tasks. The problem that Euler's method has is exactly the one that you posted about. As time goes on, it drifts further and further away from the orbit that it should be on.

With the Verlet method the approximate numerical curve is

This is clearly a much better approximation to the ideal curve.

 

[sha1000]

Just for demonstration I implemented the two above methods. I used $G=M=1$ with $r_0=(1,0)$ and $v_0=(0,1)$. I used $\Delta t = 0.1$ and simulated from $t=0$ to $t=10$. That $\Delta t$ is rather coarse, but shows the point well. I plotted the $x$ and $y$ components of $r(t)$

The ideal curves are

View attachment 284939When I use Euler's method the approximate numerical curve is
View attachment 284940
You can easily see that this deviates strongly from the ideal curve, and gets pretty bad pretty quickly. This is why Euler's method is generally a poor method to use for all but the most trivial tasks. The problem that Euler's method has is exactly the one that you posted about. As time goes on, it drifts further and further away from the orbit that it should be on.

With the Verlet method the approximate numerical curve is
View attachment 284941
This is clearly a much better approximation to the ideal curve.

Thank you Dale for your help and time you accorded to this topic. I get it much better now.

Actually what I was trying to do is to find the orbital velocity as a function of radius using this method.

For this purpose I only need to find the velocity which satisfies two conditions:
- at t=0 r=(R,0) and at t=dt r = (R,dθ);
- at t=0 V_initial is perpendicular to the R and at t=dt V'= V_initial and still perpendicular to the R;

 

[sha1000]

The idea was to take into account all the physical parameters in order to calculate the exact position and velocity change of the particle after dt. But it seems like that one cannot get an exact solution using the integration method, only an approximation.

 

[Dale]

But it seems like that one cannot get an exact solution using the integration method, only an approximation.

Yes, that is generally true.