- #1
Samit Chak
- 10
- 0
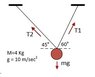
Suppose an object of mass m is hung in a steady state by two strings. One string makes an angle 60 deg. at the point of contact with the object with the horizontal line. The other string makes 45 deg.
To find the tensions in these strings (T1 and T2) we take all Horizontal Forces or their horizontal components and equate it to 0. Same thing repeated for Vertical. Then solve the equations.
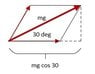
But if I consider that there is a net force in upward direction with magnitude mg which is countering gravitational force. Then can't we find the T1 and T2 as T1 = mg cos 30 and T2=mg cos 45 ? I am getting different results with these two methods. Can you pls. let me know what could be the issue here?
To find the tensions in these strings (T1 and T2) we take all Horizontal Forces or their horizontal components and equate it to 0. Same thing repeated for Vertical. Then solve the equations.
But if I consider that there is a net force in upward direction with magnitude mg which is countering gravitational force. Then can't we find the T1 and T2 as T1 = mg cos 30 and T2=mg cos 45 ? I am getting different results with these two methods. Can you pls. let me know what could be the issue here?