Calculation of the field due to a dipole at an arbitrary point

[Hamiltonian]

Homework Statement

Calculate the magnitude of the field due to a dipole at a point P which is at a distance $r$ from the midpoint of the two charges and makes an angle $\theta$ with the dipole moment Vector $P$. the distances between the two opposite charges is $a$ and $(a<<r)$.

Relevant Equations

-

I know how to derive field using $E = -\nabla V$ in polar coordinates and doing so gave me $$E = (kP/r^3)(1 + 3cos^3\theta)^{1/2}$$

now I am trying to derive $E$ at point P using the fields produced by +ve and -ve charge respectively and taking components of each along the radial direction along $r$ and perpendicular to $r$. I assumed angles $\alpha$ and $\beta$ with the perpendicular to the radial direction in hopes they get eliminated when finding $E_{net}$.

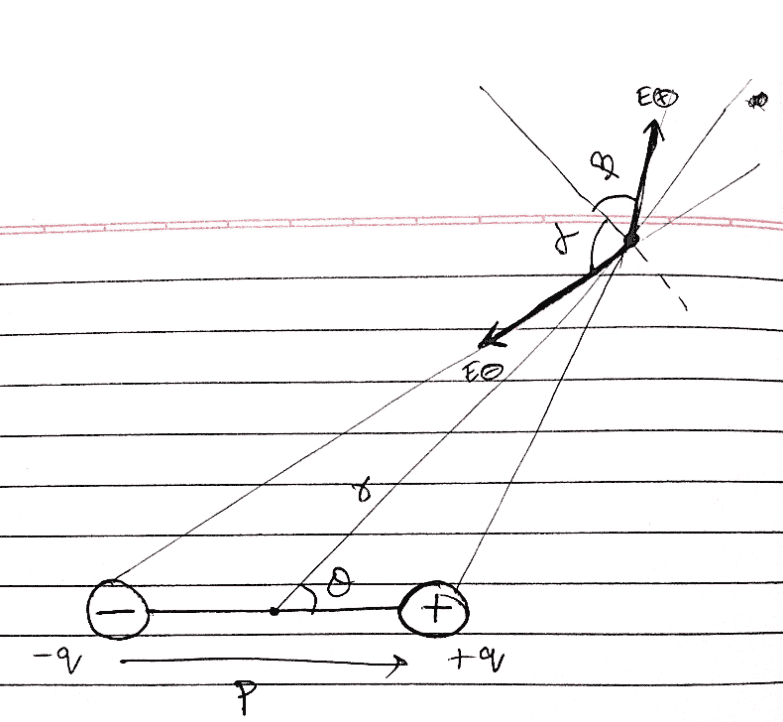
$$E_+ = \frac {kq}{r^2} (1+ (2a/r) cos\theta)$$
$$E_- = \frac {kq}{r^2} (1- (2a/r) cos\theta)$$
here $E_+$ and $E_-$ are fields due to the -ve and +ve charges at point P.
$$E_r = E_+ sin\beta - E_- simn\alpha$$
$$E_{r'} = E_+ cos\beta + E_- cos\alpha$$
here $E_r$ is the componetnt of $E_{net}$ at P along $r$ and $E_{r'}$ is the component of $E_{net}$ perpendicular to $r$.
$$| E_{net}| = \sqrt{(E_r)^2 + (E_{r'})^2}$$
I am not able to eliminate $\alpha$ and $\beta$ from the final expression for $E_{net}$.

 

[Orodruin]

I know how to derive field using E=−∇V in polar coordinates and doing so gave me E=(kP/r3)(1+3cos3θ)1/2

This doesn’t seem right. You have given a scalar, but the electric field is a vector field. Please show your work

 

[Hamiltonian]

This doesn’t seem right. You have given a scalar, but the electric field is a vector field. Please show your work

I forgot to put an arrow on top of $E$
$$\vec E = -\nabla V$$

although my doubt wasn't related to this, this is what I did
$$V_p = (kPcos\theta)/r^2$$
$$ |\vec E| = \sqrt{(-\frac{\partial V}{\partial r})^2 + (-\frac{1}{r}\frac {\partial V}{\partial \theta})^2} = \frac{kP}{r^3}\sqrt{1+3cos^2\theta}$$

 

[TSny]

.

View attachment 281253
$$E_+ = \frac {kq}{r^2} (1+ (2a/r) cos\theta)$$
$$E_- = \frac {kq}{r^2} (1- (2a/r) cos\theta)$$

I don't think the factors of 2 are correct in the right-hand sides of these two equations. Post your work if you would like us to check it.

$$E_r = E_+ sin\beta - E_- sin\alpha$$
$$E_{r'} = E_+ cos\beta + E_- cos\alpha$$

I am not able to eliminate $\alpha$ and $\beta$

Try to relate $\beta$ and $\theta$. Hint: apply the law of sines to one of the triangles in your figure.

 

[Hamiltonian]

.
I don't think the factors of 2 are correct in the right-hand sides of these two equations. Post your work if you would like us to check it.

the distance between the two opposite charges is $2a$
applying the cosine rule to both the triangles gives
$$r_+^2 = r^2 + a^2 -2arcos\theta \approx r^2 -2arcos\theta$$
$$r_-^2 = r^2 +a^2 -2arcos\theta \approx r^2 +2arcos\theta$$

also after applying the sine rule to both the triangles and making a few approximations I was able to get the required answer thanks!

 

[TSny]

the distance between the two opposite charges is $2a$

OK. In the original post, the distance is given to be $a$ rather than $2a$. That accounts for why I thought you were off by a factor of 2. I'm glad everything worked out.

 

[Orodruin]

I forgot to put an arrow on top of $E$
$$\vec E = -\nabla V$$

although my doubt wasn't related to this, this is what I did
$$V_p = (kPcos\theta)/r^2$$
$$ |\vec E| = \sqrt{(-\frac{\partial V}{\partial r})^2 + (-\frac{1}{r}\frac {\partial V}{\partial \theta})^2} = \frac{kP}{r^3}\sqrt{1+3cos^2\theta}$$

My concern was not the missing arrow, it was the fact that your computed $E$ is a scalar field and not a vector.

and doing so gave me $$E = (kP/r^3)(1 + 3cos^3\theta)^{1/2}$$

 

[Hamiltonian]

My concern was not the missing arrow, it was the fact that your computed $E$ is a scalar field and not a vector.

the question states calculate the magnitude of the electric field due to an electric dipole at a point $P$

$$|\vec E| = \frac{kP}{r^3}(1+ 3 cos^2\theta)^{1/2}$$