KedarMhaswade
- 35
- 6
- TL;DR Summary
- This post asks about the precise conversion between the 3-d Cartesian and Spherical Polar coordinates. The problem is from Anthony French's book: Newtonian Mechanics.
In Anthony French's book, Newtonian Mechanics, while explaining the non-Euclidean nature of the 3-d space, he poses a problem (I have rephrased it slightly):
Here is the figure (zoomed in):
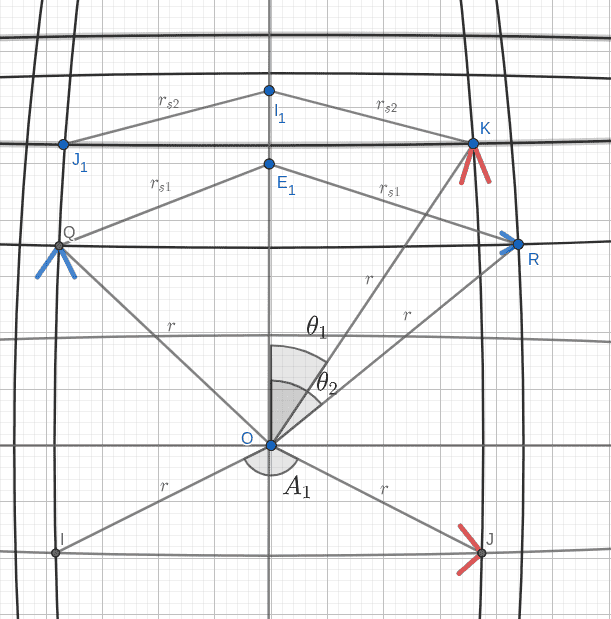
To simplify somewhat, we assume a sphere and therefore no geodesy is involved. I assume the physics convention of the Spherical Polar coordinates, i.e. the coordinates are: ##(r,\theta,\varphi)## where ##r## is the radius, ##\theta## is the polar angle, and ##\varphi## is the azimuthal angle.
My plan was to calculate Cartesian coordinates for K and R and determine the distance between the two. I guess I can make some progress on calculations, since the determination of ##r## (##6400 km##)and ##\theta_1## and ##\theta_2## appears straightforward. However, I am unsure how to calculate the ##\varphi## for the points K and R. For instance, in case of point K, ##\varphi## is different from the angle ##A_1## whose radian measure is ##\frac{1000\cdot 2\pi}{c}## where ##c## is Earth's circumference.
- Suppose you are on Earth's equator (r = 6,400 km) at the prime meridian (point I).
- You first walk along the equator 1000 miles east and reach another meridian at point J. You then walk 1000 miles north along that meridian and reach a point K (red arrows).
- You go back to point I and walk along the prime meridian 1000 north and reach a point Q on some small circle. You then walk 1000 miles east along that small circle and reach a point R (blue arrows).
Here is the figure (zoomed in):
To simplify somewhat, we assume a sphere and therefore no geodesy is involved. I assume the physics convention of the Spherical Polar coordinates, i.e. the coordinates are: ##(r,\theta,\varphi)## where ##r## is the radius, ##\theta## is the polar angle, and ##\varphi## is the azimuthal angle.
My plan was to calculate Cartesian coordinates for K and R and determine the distance between the two. I guess I can make some progress on calculations, since the determination of ##r## (##6400 km##)and ##\theta_1## and ##\theta_2## appears straightforward. However, I am unsure how to calculate the ##\varphi## for the points K and R. For instance, in case of point K, ##\varphi## is different from the angle ##A_1## whose radian measure is ##\frac{1000\cdot 2\pi}{c}## where ##c## is Earth's circumference.