- #1
Civil_Disobedient
- 15
- 0
1. Here's the problem on trig integrating that I'm struggling with (Calculus 2 btw)
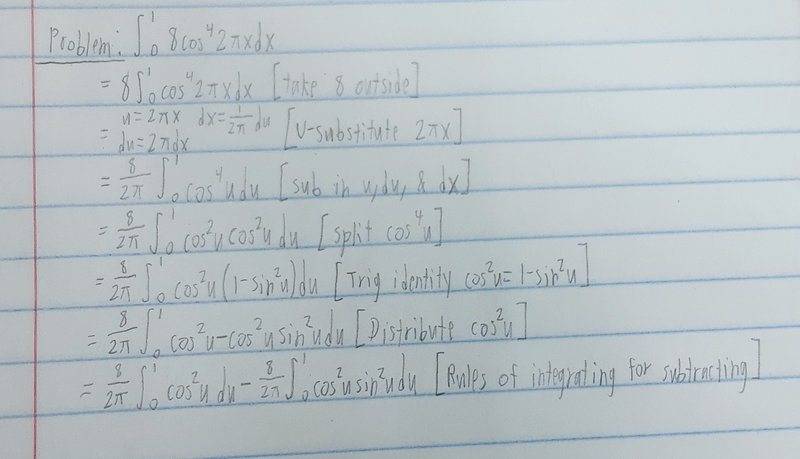
2. Wanted to see if I did everything right so far and what to do after all this. The part where I'm stuck is how to integrate (integral)cos^(2)udu and (integral)cos^(2)usin^(2)udu. I'm sure these are easy integrals, but I'm terrible with trig identities and when or how to use them. Any suggestions?
2. Wanted to see if I did everything right so far and what to do after all this. The part where I'm stuck is how to integrate (integral)cos^(2)udu and (integral)cos^(2)usin^(2)udu. I'm sure these are easy integrals, but I'm terrible with trig identities and when or how to use them. Any suggestions?
