Calculus area between two curves

[dako]

Homework Statement

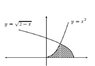
How to Find the area of ​​the shaded region in the image below:

http://i47.tinypic.com/263ed5d.jpg (without space)Hi, please help me with this:

How to find the common points in between the curves? and the area??

Homework Equations

y= x^2
y= (x-2)^(1/2)
x = 0

The Attempt at a Solution

I try to find the common point doing:

x^2 = (x-2)^(1/2) but I can't do it...

Homework Statement

Homework Equations

The Attempt at a Solution

 

[Whovian]

Simple. Split it into two halves, each of which you can calculate with a simple integral.

 

[DryRun]

dako, you can simply edit your post and attach your picture directly without having to use an external image host. I've made the attachment in this post.

There is no need to split the region, as the latter is horizontally simple.
$$\int \int \,dxdy$$

 

[dako]

Hi..! thanks! but how may I find the limits to evaluate the integrals?

 

[DryRun]

Describe the region:
For y fixed, x varies from x= to x=
y varies from y= to y=

 

[Whovian]

Hi..! thanks! but how may I find the limits to evaluate the integrals?

If you want to use a double integral, I suggest you learn a bit about multivariable calculus. Basically, if I'm understanding correctly, what sharks is saying is (in singlevariable students' terms), is that if we integrate x with respect to y, we'll get the same result. That is, take horizontal slices instead of vertical ones in the "infinite rectangles" definition of the Integral.

 

[Alcubierre]

Set the lines equal to each other to find the point of intersection. Then, integrate from 0 to that point plus from that point to the x-intercept of sqrt(2-x).

 

[dako]

This is the solution:

Using horizontal
1 Doing x= f(y)

When y=√(2-x) , x=2-y^2
When y= x^2 , x =√y

The point in common is (1,1), we must evaluate from 0 to 1 this integral:

∫ 2-y^2 - √y dy

It must be 1.

Thanks!