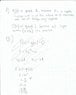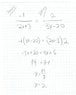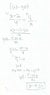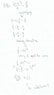Calculus - finding the minimal length between two functions

[Femme_physics]

Homework Statement

http://img823.imageshack.us/img823/6708/calc099.jpg

In this graph are 2 functions

http://img402.imageshack.us/img402/6/functions000.jpg

In the domain of x > 0

A) Which of the graphs, I and II is of the function f(x), and which is of g(x)? Explain (I answered this)

B) A is a point on graph I, and B is a point on graph II so the section AB is parallel to the Y axis (see graph). Find the x coordinate of the points A and B that for them the length AB is minimal.

The Attempt at a Solution

Attached. I answered A, B is the tricky one for me. I tried to pitch an answer. The manual tells me I'm wrong.

 

[I like Serena]

Hi PG, :)

You set the derivative of f(x) equal to the derivative of g(x).
This will solve to the x coordinate where the slopes of f(x) and g(x) are parallel.
However, that is not what the problem asks.

First you need to think up a formula for the length of AB as a function of x.
This would be the difference of f(x) and g(x).

Then you can take the derivative and solve for being equal to zero.

 

[Femme_physics]

Hey :)

I tried a few times and wrinkled off a few papers (calculus is the biggest problem the rainforest conservation efforts is dealing with) until *I think* I got the answer.

Did I make the right moves? Is that right?

 

[I like Serena]

Hey :)

I tried a few times and wrinkled off a few papers (calculus is the biggest problem the rainforest conservation efforts is dealing with) until *I think* I got the answer.

:)

Did I make the right moves? Is that right?

Not quite.

AB = f(x) - g(x)

In your problem the domain is x > 0, so any solution of x that is negative does not count.

You need to fill in your solution for x in the formula for AB, which is the difference in y coordinates.

Note also that your derivative of f(x) is not quite right (rushing again?)

 

[Femme_physics]

Note also that your derivative of f(x) is not quite right (rushing again?)

There's rushing, and there's not knowing. I'm not sure what's the case here.

You need to fill in your solution for x in the formula for AB, which is the difference in y coordinates.

Okay, I "think" I now have done that. Does this make sense?

 

[I like Serena]

There's rushing, and there's not knowing. I'm not sure what's the case here.

Okay, I "think" I now have done that. Does this make sense?

Yes, it makes sense... but...

You started with:
f(x)-g(x)=(x-2)/4 - 4/x

And then you converted it to:
y(x)=x(x-2) - 4(4)

Apparently you multiplied by x respectively by 4, which you would do to add two fractions.
That would be ok, except that then you threw the denominator out, which you're not allowed to do.

So what you should have is:
y(x)=(x-2)/4 - 4/x

What you did after was entirely correct, just with the wrong formula for y(x).

 

[Femme_physics]

Yes, it makes sense... but...

You started with:
f(x)-g(x)=(x-2)/4 - 4/x

And then you converted it to:
y(x)=x(x-2) - 4(4)

Apparently you multiplied by x respectively by 4, which you would do to add two fractions.
That would be ok, except that then you threw the denominator out, which you're not allowed to do.

So what you should have is:
y(x)=(x-2)/4 - 4/x

What you did after was entirely correct, just with the wrong formula for y(x).

Thanks! I must have forgotten how to do fractions correctly! (going back to 3rd grade now :P ) The thing is I seem to recall that if the denominator was the same you can just forgo it. It's just that I don't remember when I did it. Am I imagining it?

 

[I like Serena]

Thanks! I must have forgotten how to do fractions correctly! (going back to 3rd grade now :P ) The thing is I seem to recall that if the denominator was the same you can just forgo it. It's just that I don't remember when I did it. Am I imagining it?

I can think of a reason to do it.
You would do something like that if you're solving an equation that is equal to zero.
But even then you need to be careful and I think we'll get back to that sooner of later.

Anyway, you're not solving an equation that is equal to zero here - you're calculating the derivative of a function.

 

[Femme_physics]

I can think of a reason to do it.
You would do something like that if you're solving an equation that is equal to zero.
But even then you need to be careful and I think we'll get back to that sooner of later.

Anyway, you're not solving an equation that is equal to zero here - you're calculating the derivative of a function.

Hmm, then how come in this case I dispose of the denominator and get the right answer?

 

[I like Serena]

Hmm, then how come in this case I dispose of the denominator and get the right answer?

3 differences.

First this is an equation (not equal to zero) where you multiply left and right with 24. This is proper.
Note that if the right side had been zero, it would have remained zero, which is also proper.

Second, you're not taking a derivative here.

Third, you're not multiplying by something which involves "x".
When "x" (or any variable) is involved there are a few extra rules that need to be taken care of.

 

[Femme_physics]

Second, you're not taking a derivative here.

But an equation is an equation, regardless of how we've gotten to that equation, right?

They wouldn't give me an equation telling me, "oh, and we've gotten to take equation by taking the derivative."

That doesn't matter, I solve it with the same old algebra. Derivative doesn't have its own algebra while doing equations, right?

Third, you're not multiplying by something which involves "x".

Attached!

 

[I like Serena]

But an equation is an equation, regardless of how we've gotten to that equation, right?

They wouldn't give me an equation telling me, "oh, and we've gotten to take equation by taking the derivative."

That doesn't matter, I solve it with the same old algebra. Derivative doesn't have its own algebra while doing equations, right?

What I'm saying is that the derivative of (x-2)/4 - 4/x is significantly different from the derivative of x(x-2) - 4(4).

You're right in the fact that we solve the derivative for being equal to zero.
But you'll find that the solution is both cases is different.

Attached!

The catch here is that if the solution for x would have been -3/2 (which of course it isn't), that it wouldn't have been a proper solution, because if you would fill it in in your original equation, the left hand side is undefined (check it!)

So your method to solve the equation is good.
The catch is that you have to check afterward if your solution for x will work if you substitute it in the original equation (in this case it works, in other cases it won't).

To illustrate this, can you find the flaw in the following proof?

 

[Femme_physics]

What I'm saying is that the derivative of (x-2)/4 - 4/x is significantly different from the derivative of x(x-2) - 4(4).

You're right in the fact that we solve the derivative for being equal to zero.
But you'll find that the solution is both cases is different.

Oh yes, I agree with that :)

To illustrate this, can you find the flaw in the following proof?

Yes, "x" should be squared!

So I keep the denominator only in cases where the equation equals zero?


And by the way-- I attached my latest attempt at solving for the minimal length

 

[ideasrule]

This shouldn't be a long problem. You've already gotten:

AB=(x-2)/4 - 4/x

Now we need to take its derivative. The first term, (x-2)/4, is a line and can be rewritten as x/4 - 1/2. What's the derivative of a line? The second term is 4/x. What's the derivative of that? After you get the derivative of AB, set the result to 0 and solve for x. You don't need to put (x-2)/4-4/x under a common denominator. In fact, doing so will make the problem much more tedious than it needs to be.

 

[Femme_physics]

I'm getting to the point of no solutions (if I keep the denominator 4x^2)

If I don't I get the same solution I got in the last attachment, which the length = 4.25

 

[Mentallic]

Well obviously the no solutions answer you're getting is wrong, because there is a minimum distance present. We can see it visually.

g(x)=\frac{-4}{x}

so then

f(x)-g(x)=\frac{x-2}{4}+\frac{4}{x}

edit: p.s. In your last attachment you didn't take the derivative correctly

The derivative of y=\frac{f(x)}{g(x)} is not \frac{dy}{dx}=\frac{f'(x)}{g'(x)} but rather \frac{dy}{dx}=\frac{g(x)\cdot f'(x)-f(x)\cdot g'(x)}{[g(x)]^2}

 

[Femme_physics]

Eek! I didn't know you have to use the quotient rule in our relative simple studies of basic calculus! Isn't there a shortcut to avoid all that?

I was once told from a PhD in math that a good mathematician is the lazy mathematician!

 

[I like Serena]

Eek! I didn't know you have to use the quotient rule in our relative simple studies of basic calculus! Isn't there a shortcut to avoid all that?

I was once told from a PhD in math that a good mathematician is the lazy mathematician!

In your last scan there was no need to use the quotient rule and you didn't.
You only need to correct the minus sign as Mentallic suggested.

[edit]My fault, I overlooked the minus sign earlier ;)[/edit]

 

[Mentallic]

In your last scan there was no need to use the quotient rule and you didn't.]

I meant the scan in post #13

Eek! I didn't know you have to use the quotient rule in our relative simple studies of basic calculus! Isn't there a shortcut to avoid all that?

Yes, don't find a common denominator for the expression.

 

[Femme_physics]

Yes, don't find a common denominator for the expression.

In this case I'm not sure how to solve for the derivative = 0 without having a quadratic equation, since I need a positive exponent that's not under the fraction. For that, I need to take a common denominator.

 

[I like Serena]

In this case I'm not sure how to solve for the derivative = 0 without having a quadratic equation, since I need a positive exponent that's not under the fraction. For that, I need to take a common denominator.

That's ok. :)
You can use a common denominator if you want.
Equivalently you can multiply left and right with 4x² which works out the same.

 

[Femme_physics]

Equivalently you can multiply left and right with 4x² which works out the same.

Wait, but will that cancel the denominator? Right side equals zero anyway, so it will remain zero. By multiplying both side, it's as though I just cancel out the denominator on one side! That doesn't seem quite right.

 

[I like Serena]

Wait, but will that cancel the denominator? Right side equals zero anyway, so it will remain zero. By multiplying both side, it's as though I just cancel out the denominator on one side! That doesn't seem quite right.

Is right anyway.

 

[Femme_physics]

Are you telling me that WITH the denominator and without the denominator, it's the same thing?

(gotta go, will reply later when can. Thank you ever so much!)

 

[Mentallic]

In this case I'm not sure how to solve for the derivative = 0 without having a quadratic equation, since I need a positive exponent that's not under the fraction. For that, I need to take a common denominator.

You can take a common denominator whenever you want, but for the expression f(x)-g(x)=\frac{x-2}{4}+\frac{4}{x} it is easier to take the derivative if you don't take a common denominator. Once you take the derivative and set it to zero, you can find a common denominator if you like. The difference between an equation (something = something else) and an expression (y= something), in order to keep an equation balanced, whatever you do to one side you need to do to the other side, but with an expression you don't do anything to the other side, you could, but then you would have things like 2y and y² on the left side, and you don't want to do that. Instead, you keep things balanced by having a common denominator etc. WITHOUT getting rid of the denominator.

Are you telling me that WITH the denominator and without the denominator, it's the same thing?

(gotta go, will reply later when can. Thank you ever so much!)

If one side is equal to zero, yes, a fraction is only zero if its numerator is zero, so it doesn't matter what its denominator is (except in certain cases where the denominator does affect the numerator, but don't worry about those for now).

 

[Femme_physics]

Wow, Mentallic, you're incredible. Thank you ever so much for this detailed, clear explanation. I will cherish it. :) Exactly what I needed to clear up that little confusion I had. Brilliant! When I get back home I will see if I can finally get the right answer to this pesky question!


Much appreciated!

(found time to reply since my student is late :) )

 

[Mentallic]

Wow, Mentallic, you're incredible. Thank you ever so much for this detailed, clear explanation. I will cherish it. :) Exactly what I needed to clear up that little confusion I had. Brilliant! When I get back home I will see if I can finally get the right answer to this pesky question!


Much appreciated!

(found time to reply since my student is late :) )

You're welcome!

 

[ideasrule]

Sorry for not catching the sign error, BTW.

 

[Femme_physics]

Hmm...so without the denominator in my last attachment I get 4i, -4i

I've been really killing myself. Can anyone just please show me the solution (at least from how far I've gotten without making a mistake)?

 

[I like Serena]

Hmm...so without the denominator in my last attachment I get 4i, -4i

I've been really killing myself. Can anyone just please show me the solution (at least from how far I've gotten without making a mistake)?

I'm going in for the final kill!

You started with:

AB=\frac {(x-2)} 4 - \frac 4 x​

Could you instead start with:

AB=\frac {(x-2)} 4 + \frac 4 x​

And do exactly the same thing?