- #1
1LastTry
- 64
- 0
Homework Statement
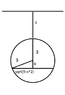
Find the force acting on one end of a cylindrical drum with 3m. If the rim is submerged horizontally into water so that the bottom is 10m deep.
Homework Equations
A(x) - Area
p(x) - Pressure = density * Depth
g= 9.8
A(x) =2[itex]\sqrt{9-x^{2}}[/itex]
P(x) = 1000(7+x) * g
dF = 2000*g*[itex]\sqrt{9-x^{2}}[/itex](7+x) dx
F = 2000g [itex]\int^{3}_{-3}[/itex][itex]\sqrt{9-x^{2}}[/itex](7+x)dx
Finally, my question is why is the limit goes from -3 to 3? Where does it come from? A picture is in the attachment.
The Attempt at a Solution
I have no clue about this. I am ok with Integrals and finding the equations for the problem. However, I am not sure on how to find the limits of the definite integral, so hints and information on how to find the limits (such as -3 to 3) is very much appreciated. Thank you for your time.
Attachments
Last edited: