Calculus Tangent Line: Find Parameter k | Camille's Q&A

[MarkFL]

Here is the question:

Calculus tangent line?

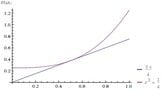
If the line 3x-4y=0 is tangent in the first quadrant to the curve y=x^3+k then k is
(a)1/2
(b)1/4
(c)0
(d)-1/8
(e)-1/2
Could you please show work because I am so lost

I have posted a link there to this topic so the OP may see my work.

 

[MarkFL]

Hello Camille,

Let's begin by equating the derivative of the curve to the slope of the tangent line. The tangent line may be written as $$y=\frac{3}{4}x$$ hence:

$$\frac{3}{4}=3x^2$$

$$x^2=\frac{1}{4}$$

Since we are interesting in the first quadrant solution, we take the positive root:

$$x=\frac{1}{2}$$

Now, the tangent line and the curve have then tangent point in common, and so using the tangle line, we know this point is:

$$\left(\frac{1}{2},\frac{3}{4}\cdot\frac{1}{2} \right)=\left(\frac{1}{2},\frac{3}{8} \right)$$

Hence, we must have:

$$y\left(\frac{1}{2} \right)=\left(\frac{1}{2} \right)^3+k=\frac{1}{8}+k=\frac{3}{8}$$

And so we must have:

$$k=\frac{1}{4}$$

Here is a plot of the curve $$y=x^3+\frac{1}{4}$$ and the tangent line $$y=\frac{3}{4}x$$ for $0\le x\le1$:

View attachment 1322