MHB Can a bipartite graph have two non-connected parts?

  • Thread starter Thread starter find_the_fun
  • Start date Start date
  • Tags Tags
    Graph parts
Click For Summary
A bipartite graph can indeed be disconnected, allowing for multiple non-connected components. Each component can still maintain the bipartite property, meaning it can be divided into two distinct sets of vertices. The notation $G=(U,V,E)$ is used to represent the graph's bipartition, which can vary if the graph is not connected. Therefore, the example of vertices A and B connected to C and D illustrates a valid bipartite structure. Understanding these properties is crucial for applications involving bipartite graphs.
find_the_fun
Messages
147
Reaction score
0
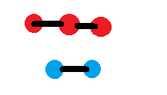
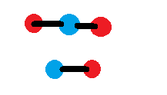
For example vertice A connected to vertice B and vertice C connected to vertice D? Would this be considered two different graphs? Here is a graph, would it be bipartite?
View attachment 1314
 

Attachments

  • graph.png
    graph.png
    445 bytes · Views: 101
  • graph.png
    graph.png
    463 bytes · Views: 99
Last edited:
Physics news on Phys.org
Re: can a bipartite graph have two not connected parts?

A bipartite graph can be disconnected. Wikipedia says: "One often writes $G=(U,V,E)$ to denote a bipartite graph whose partition has the parts $U$ and $V$, with $E$ denoting the edges of the graph. If a bipartite graph is not connected, it may have more than one bipartition; in this case, the $(U,V,E)$ notation is helpful in specifying one particular bipartition that may be of importance in an application".
 

Thread 'A variant of the Monty Hall problem'

There is a nice little variation of the problem. The host says, after you have chosen the door, that you can change your guess, but to sweeten the deal, he says you can choose the two other doors, if you wish. This proposition is a no brainer, however before you are quick enough to accept it, the host opens one of the two doors and it is empty. In this version you really want to change your pick, but at the same time ask yourself is the host impartial and does that change anything. The host...
View full post »

Similar threads

MHB Understanding Two Graph Theory Problems
  • · Replies 2 ·
Replies
2
Views
2K
MHB How many new branches will the complement graph of a deleted edge have?
  • · Replies 11 ·
Replies
11
Views
2K
MHB How many edges does the graph have?
  • · Replies 4 ·
Replies
4
Views
2K
A Concrete examples of randomness in math vs. probability theory
  • · Replies 11 ·
Replies
11
Views
3K
MHB Statement of a theorem due to Bondy.
  • · Replies 4 ·
Replies
4
Views
2K
MHB Graph: showing that diameter is greater than average pairwise distance
  • · Replies 4 ·
Replies
4
Views
3K
MHB Proving K-Extendability of a Bipartite Graph
  • · Replies 1 ·
Replies
1
Views
1K
I Finding the dependence of maximum vertex degree on k-colorability
  • · Replies 1 ·
Replies
1
Views
2K
MHB Graph Theory Proof: Connectivity of G Proven
  • · Replies 3 ·
Replies
3
Views
2K
MHB Is HSC NP-Complete in Graph Theory?
  • · Replies 1 ·
Replies
1
Views
2K