Can a scalar field model account for the cosmic redshift?

[Tertius]

TL;DR Summary

A minimally coupled scalar field is easily shown to replicate a cosmic fluid. But can it account for the cosmological redshift?

A minimally coupled scalar field can model a cosmological fluid model where

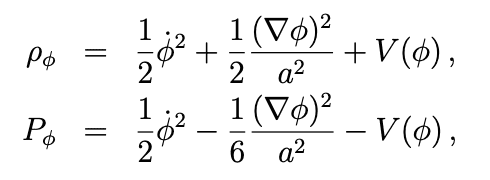
And where the equation of state can be the standard $\omega = \frac {p} {\rho}$

I can see how this does a fine job modeling matter, because as the scale factor increases, the density will go as $\frac {1} {a^3}$. However, is it possible for it to account for the redshift, where photon energy density goes as $\frac {1} {a^4}$.

Last, and somewhat related questions. Because all known particles in the universe follow the energy-momentum relation, and thus the Klein-Gordon equation, is is possible to use the KG equation (or really just a classical scalar field) to model all the contents of the universe? This is what got me thinking about a scalar field reproducing the cosmological redshift.

 

[strangerep]

Which textbook(s) on Cosmology, GR, Quantum Mechanics, Quantum Field Theory and the Standard Model have you studied already?

Your question suggests you haven't studied any such textbooks in depth since you're trying to use a scalar field to model fields with intrinsic spin. This fails immediately.

 

[Tertius]

I have used Weinberg and Carroll for GR/cosmology. Only introductory particle physics from Griffiths.

From what I understand, every solution to the dirac equation (and I imagine spin-1 fields as well) are also solutions to the KG equation. So why can't you use the KG equation as a scalar model (obviously not accounting for spin) for spin particles as well? Meaning only as a model of the energy/momentum relation that all fields follow.

Also, I am most interested in the first question, can a scalar field model a cosmological redshift?

 

[strangerep]

From what I understand, every solution to the dirac equation (and I imagine spin-1 fields as well) are also solutions to the KG equation. So why can't you use the KG equation as a scalar model (obviously not accounting for spin) for spin particles as well? Meaning only as a model of the energy/momentum relation that all fields follow.

Bose-Einstein statistics are rather different from Fermi-Dirac statistics. This has consequences when trying to model the expansion of the universe.

Also, I am most interested in the first question, can a scalar field model a cosmological redshift?

If a field has an energy density $\rho$, you can stick it into the Einstein equations to get the Friedman equations and obtain an evolving relationship between the Hubble parameter and the energy density. The real issue is whether the detailed evolution of the Hubble parameter matches what we observe at different epochs in the history of the universe. E.g., a radiation-dominated universe behaves differently from a matter-dominated universe.

"Modern Cosmology" by Dodelson & Schmidt treats all this in far more depth than I can summarize here.

 

[Tertius]

I've only studied maxwell-boltzmann based stat mech, so i'll need to look into these.

With the red shift, are you saying 'sure you can use a scalar field to model even the radiation, but the question is whether you have the correct amounts of matter and radiation'?

Thanks for the book suggestion. I am looking for something more in depth like that.

 

[strangerep]

With the red shift, are you saying 'sure you can use a scalar field to model even the radiation, but the question is whether you have the correct amounts of matter and radiation'?

No, I'm saying you'd barely even get to 1st base -- assuming you're trying to construct a realistic model. Photons are spin-1, fermions are spin-1/2, scalars are spin-0. They're not interchangeable.

 

[Tertius]

In terms of a cosmic fluid modeled using GR, what exactly would be incorrect if you used a scalar field to model a radiation field?

Surely the energy density and pressures would be correct (and traceless).

 

[vanhees71]

In cosmology you make the ansatz, based on the Cosmological principle, that the large-scale-averaged spacetime is described by a Robertson-Walker-Friedmann-Lemaitre metric. Einstein's field equation then tells you that the energy-momentum tensor is that of an ideal fluid (including also "radiation", i.e., massless em. fields as a possibility). Besides the Einstein equations you only need the equation of state from the given model (ideal gas of massive particles, radiation, and a cosmological constant aka dark energy). By solving Einstein's field equation then you automatically have also solved for the equation of motion of the ideal fluid. That's what you finally only need is the equation of state and the Friedmann equations for the scale parameter, $a(t)$ in the FLRW metric.

 

[Tertius]

Ok I see. So the scalar field is typically only used as an inflation field or as a cosmological constant because a slowly varying scalar field has $\rho = -p$.

And the equations of motion don't need to come from a Lagrangian of the particular component of the fluid, because that EOM is determined as a function of the equation of state chosen?

And the equation of state chosen implicitly includes how the material changes with the expansion factor.

So basically, using a scalar field to try and model everything would not work because the $T_{00}$ component of the energy momentum tensor does not actually include the scale factor, so it can only behave like a cosmological constant, assuming it is slowly varying.

 

[strangerep]

In terms of a cosmic fluid modeled using GR, what exactly would be incorrect if you used a scalar field to model a radiation field?

They behave differently under scale changes (i.e., as the universe expands).

The energy density of ordinary matter scales as $a^{-3}$, whereas the energy density of radiation scales as $a^{-4}$, where $a(t)$ is the usual time-dependent scale factor in the FLRW metric.

So basically, using a scalar field to try and model everything would not work because the component of the energy momentum tensor does not actually include the scale factor, so it can only behave like a cosmological constant, assuming it is slowly varying.

"Dark energy", i.e., the cosmo constant, scales differently from either of the above forms of energy density, being constant.

 

[Tertius]

Great. Thanks for the helpful answers. I see why my first question seemed out of place.

One last thing to make sure: it is impossible to construct a scalar field (from a Lagrangian) that scales as $a^{-4}$? or it is just totally unnecessary but possible?

 

[strangerep]

One last thing to make sure: it is impossible to construct a scalar field (from a Lagrangian) that scales as $a^{-4}$? or it is just totally unnecessary but possible?

It sure seems to be unnecessary for realworld physics. Is it absolutely impossible? That's an impossible question to answer. Different types of matter tend to have different equations of state (relationships between energy and pressure), which is key to determining their scaling behaviour in an expanding universe. Dodelson's sect 2.3 ("Evolution of Energy") explains this quite well.

 

[PeterDonis]

it is impossible to construct a scalar field (from a Lagrangian) that scales as $a^{-4}$?

Scaling as $a^{-4}$ requires the equation of state $P = \rho / 3$. What do the equations you posted for $\rho$ and $P$ say? Is that equation of state possible?

 

[PeterDonis]

Different types of matter tend to have different equations of state (relationships between energy and pressure)

Yes, and for a scalar field we have known equations for both of those; they are in the OP of this thread. So the question should be answerable for this particular case.

 

[PeterDonis]

A minimally coupled scalar field can model a cosmological fluid model where
View attachment 323638

Shouldn't the factor in the second term of $P_\phi$ be $1/2$ instead of $1/6$?

 

[PeterDonis]

I can see how this does a fine job modeling matter, because as the scale factor increases, the density will go as $\frac {1} {a^3}$.

But that in itself is not enough to model "matter"; the pressure also has to be zero. But it isn't.

 

[Tertius]

Shouldn't the factor in the second term of $P_\phi$ be $1/2$ instead of $1/6$?

Yes, that was a typo.

 

[Tertius]

Scaling as $a^{-4}$ requires the equation of state $P = \rho / 3$. What do the equations you posted for $\rho$ and $P$ say? Is that equation of state possible?

From a simple calculation, in order for a homogeneous, isotropic scalar field to have that equation of state, the $V[\phi]$ function would have to be equal to $1/4 \dot{\phi}^2$. It seems this would be a very strange potential function because it is of the exact same form as the kinetic. Probably a nonsensical field because if you put that potential into the Lagrangian to rework the EOM, it would just be a constant $1/4$.

 

[PeterDonis]

From a simple calculation, in order for a homogeneous, isotropic scalar field to have that equation of state, the $V[\phi]$ function would have to be equal to $1/4 \dot{\phi}^2$.

That's not possible. $V$ can't be a function of $\dot{\phi}$, only of $\phi$.

 

[Tertius]

That's not possible. $V$ can't be a function of $\dot{\phi}$, only of $\phi$.

Makes sense. I suppose in this case then it wouldn't be possible to have $P=\rho/3$.

 

[PeterDonis]

I suppose in this case then it wouldn't be possible to have $P=\rho/3$.

That's correct. The only possibilities are $P = - \rho$ (in the limit $\dot{\phi} \to 0$, as you said earlier in the thread), which means $\rho$ is constant (does not scale at all with $a$), or no well-defined value of $w$ at all, because the ratio $P / \rho$ does not give a constant but varies from point to point in spacetime.