Can a voltage test source help solve for Rth in a complex Thevenin's circuit?

[SixOnTheBeach]

Homework Statement

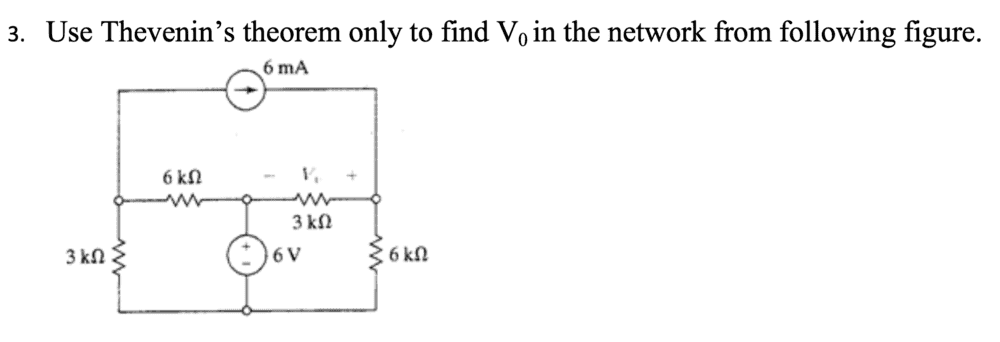
Use Thevenin’s theorem only to find V0 in the network from the following figure.

Relevant Equations

Thevenin's theorem, KCL, KVL

So I've been absolutely stumped on this one. I've tried about a million different things but none of them have seemed right. A combination of the odd layout of the circuit, and a combined voltage/current source are making things really complicated for me. I'm somewhat sure the R_Th is 15kΩ due to the resistors being in series when traversing from A to B. But that's really all I've got and I'm not even sure if that's right. I did figure out a couple things but I'm not so sure if they're helpful. I found the current between the voltage source and A on the load resistor is 2.667mA, so my best guess is that the voltage across should be that multiplied by the 6kΩ resistor to be 16V? But then I'm not sure if the 6mA current source would be going through from B to A and subtract from that. I've spent all day trying to figure this out so I'd really appreciate some guidance on how to tackle a problem like this. Thank you!

 

[phinds]

You keep talking about A and B, but I don't see those on the drawing.

 

[alan123hk]

I'm somewhat sure the RTh is 15kΩ due to the resistors being in series when traversing from A to B.

Except not sure where the two points A and B you mentioned are, I tried many combinations, but I still can't get Rth = 15K. Can you provide more information for reference?

 

[gneill]

In order to explore where you might be running into difficulty, perhaps you might begin by describing your understanding of the prescribed method for find the Thevenin equivalent of a circuit. For now, we assume that only fixed value sources are in play -- no dependent sources or other complications.

 

[DaveE]

Honestly, I am more than willing to help with these problems. Except... I am not very motivated to hack thorough the word salad you present as your attempt at a solution. If you think nodes A & B are important, why don't you tell us what they are. So, more sketches of schematics, with components, nodes sources, named with labels so we are talking about the same things. I suspect most of your confusion lies in trying to jump to an answer without a methodical documentation of the steps (again: schematics!). I would add that your instructor isn't helping here, two 3K resistors and two 6K resistors without names (we call names "reference designators" in EE world)?

OK, so Thevenin's theorem breaks the problem down into finding the voltage across the load with the load removed (∞ resistance). And the "driving point impedance" at the load, i.e. the impedance measured across the load terminals, again with the load removed. Note that the impedance (resistance) of a voltage source is zero, a short circuit. The impedance (resistance) of a current source is infinite, an open circuit.

Which of these two parts are you having problems with? Please show your work.

 

[Joshy]

I think OP is referring to A and B as + and - across the load.

The only way I could "imagine" $15 k\Omega$ is $3 k\Omega + 6 k\Omega + 6 k\Omega$. That does not look right to me. I think that would happen if that voltage source were a current source, but it's not.

What did you do in order to get $R_{th}$? Can you draw the schematic for $R_{th}$?

Spoiler

Something really nice happens when you're looking at the $R_{th}$ circuit :) When I draw the X I'm meaning to open circuit there, and the thick straight line | is a short circuit.

Spoiler

Something very nice also happens when you solve for your $V_{OC}$. Where does all of the current go from the current source when you remove that $3k\Omega$ resistor between the + and -? From there you will know the voltage drop across the $6k\Omega$ resistor and you know the voltage across the voltage source. If you know the voltages of both, then I would imagine you would know what the voltage difference across + and - would be.

Spoiler

You could move the "ground" where I drew it if you wanted... it's only a reference and so you can move it where it is most convenient for you (some people like to draw it where the VMINUS is at).

 

[SixOnTheBeach]

I think OP is referring to A and B as + and - across the load.

The only way I could "imagine" $15 k\Omega$ is $3 k\Omega + 6 k\Omega + 6 k\Omega$. That does not look right to me. I think that would happen if that voltage source were a current source, but it's not.

What did you do in order to get $R_{th}$? Can you draw the schematic for $R_{th}$?

Spoiler

Something really nice happens when you're looking at the $R_{th}$ circuit :) When I draw the X I'm meaning to open circuit there, and the thick straight line | is a short circuit.

View attachment 279980

Spoiler

Something very nice also happens when you solve for your $V_{OC}$. Where does all of the current go from the current source when you remove that $3k\Omega$ resistor between the + and -? From there you will know the voltage drop across the $6k\Omega$ resistor and you know the voltage across the voltage source. If you know the voltages of both, then I would imagine you would know what the voltage difference across + and - would be.

Spoiler

You could move the "ground" where I drew it if you wanted... it's only a reference and so you can move it where it is most convenient for you (some people like to draw it where the VMINUS is at).

View attachment 279981

Yeah I'm sorry maybe I should've clarified but every example I saw listed across the load as A and B so I assumed it would be obvious, that's on me

 

[SixOnTheBeach]

Except not sure where the two points A and B you mentioned are, I tried many combinations, but I still can't get Rth = 15K. Can you provide more information for reference?

I was adding the 3 resistors in series with the load resistor removed. I assumed this because two of the resistors were in series going into A, and then the third resistor seemed to be in series after B. I have now found out the true resistance is 6kΩ, although I'm not sure why.

 

[SixOnTheBeach]

Honestly, I am more than willing to help with these problems. Except... I am not very motivated to hack thorough the word salad you present as your attempt at a solution. If you think nodes A & B are important, why don't you tell us what they are. So, more sketches of schematics, with components, nodes sources, named with labels so we are talking about the same things. I suspect most of your confusion lies in trying to jump to an answer without a methodical documentation of the steps (again: schematics!). I would add that your instructor isn't helping here, two 3K resistors and two 6K resistors without names (we call names "reference designators" in EE world)?

OK, so Thevenin's theorem breaks the problem down into finding the voltage across the load with the load removed (∞ resistance). And the "driving point impedance" at the load, i.e. the impedance measured across the load terminals, again with the load removed. Note that the impedance (resistance) of a voltage source is zero, a short circuit. The impedance (resistance) of a current source is infinite, an open circuit.

Which of these two parts are you having problems with? Please show your work.

I would have shown my work, but embarrassingly I don't really have anything to show... All I've done is remove the power sources and the load resistor. And yes, my instructor for this class is really awful, that is why I am struggling so much with these topics as he is pretty useless in helping and it is incredibly difficult to gain a good understanding of the topics by myself.

I am struggling to figure out how one goes about adding these resistors when there is no clear way to divide up the circuit and there are multiple paths from A to B(V- to V+). The two paths from A to B are either through all 3 resistors or simply through the 6k resistor if taking the short circuited path. I did not think it was possible to combine both paths(in parallel) as they both run through the 6k resistor right before B. So I figured the only way to solve this must be to take them in series.

As for the voltage across the load resistor, where I am running into difficulty is that I fail to understand how the two power sources interact. From a look at someone else's work, I believe the correct answer is to simply subtract the 36V source going into B(the 6mA current source * the 6k resistor) from the 6V source going into A to arrive at -30V. However, I don't understand why the current source would not also be interfering from point A as well, as I know that it DOES affect the current flowing through there.

I'm sorry if this is still too word salady, I can attempt to draw a diagram explaining what I mean if it's still necessary.

EDIT: I think I explained myself better in my last response to Joshy

 

[SixOnTheBeach]

I think OP is referring to A and B as + and - across the load.

The only way I could "imagine" $15 k\Omega$ is $3 k\Omega + 6 k\Omega + 6 k\Omega$. That does not look right to me. I think that would happen if that voltage source were a current source, but it's not.

What did you do in order to get $R_{th}$? Can you draw the schematic for $R_{th}$?

Spoiler

Something really nice happens when you're looking at the $R_{th}$ circuit :) When I draw the X I'm meaning to open circuit there, and the thick straight line | is a short circuit.

View attachment 279980

Spoiler

Something very nice also happens when you solve for your $V_{OC}$. Where does all of the current go from the current source when you remove that $3k\Omega$ resistor between the + and -? From there you will know the voltage drop across the $6k\Omega$ resistor and you know the voltage across the voltage source. If you know the voltages of both, then I would imagine you would know what the voltage difference across + and - would be.

Spoiler

You could move the "ground" where I drew it if you wanted... it's only a reference and so you can move it where it is most convenient for you (some people like to draw it where the VMINUS is at).

View attachment 279981

Sorry if I've been repetitive at all, I've just been trying to respond to everyone. So as for the resistance, I don't quite understand what that nice thing is haha. I drew my diagram exactly as you have it! But does the path merely take the short circuit route and through your R1 as it's the path of least resistance? This is what was confusing me there. I assumed that the path would either go through all 3 resistors(leading to my answer of 15k) or merely through the short circuit and go through R1. I wasn't sure how to reconcile this; my thinking was do I simply pick one path or attempt to combine them in parallel?

As for the voltage source, I do understand what you're saying, and I can confirm this is the right answer. But I guess I just wanted to understand WHY that is. I know the current source affects the current going through the voltage source, and so I wanted to understand why it would not affect both A and B(by bolstering the voltage source) and... cancel out somewhat? I'm not exactly sure. Does that make sense?

 

[Joshy]

When solving for $R_{th}$ would putting a voltage test source like $V_{test}$ in place of the + and - be helpful? You can solve for the current and use Ohm's law to get $R_{th}$.