Can Bessel Functions be Simplified for Numerical Integration?

[Astaroth.]

Hello, need your help.

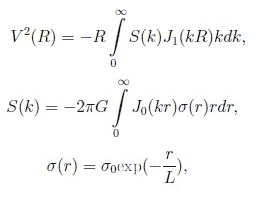
J_1 and J_0 - Bessel function
Necessary to solve analytically or to be able to simplify the numerical solution.

 

[JJacquelin]

The analytic solution for S(k) is given in the joint page.
It was obtained thanks to a known Hankel transform.
Then, for the analytic computation of V(R), another Hankel transform is needed, which I have'nt available. This will require more research. Sorry, I have not enough time now. I will look again within a few days.

 

[Astaroth.]

Thank you. I have been modeling the rotation of galaxies.
The journal «Freeman, K. C. Astrophysical Journal, vol. 160, p.811» http://articles.adsabs.harvard.edu//full/1970ApJ...160..811F/0000813.000.html described, but I need for different density profiles $\sigma$.
$\sigma (r)) = \sigma_{0} \exp(-\frac{r}{L})$
and
$\sigma (r) = \sigma (Rt)*(1+(Rt-r)/SCL)= \sigma_{0} * \exp(-\frac{Rt}{L})*(1+(Rt-r)/SCL)$
Where Rt - radius of truncation. SCL - scale truncation

 

[JJacquelin]

Finally, it was not so arduous than I thought first.
The result is expressed in terms of Bessel functions (in attachment)

 

[Astaroth.]

Thank you very much.
And if the $\sigma (r) = \sigma_ {0} * \ exp (- \frac {Rt} {L}) * (1 + (Rt-r) / SCL)$

The result will differ greatly?

 

[JJacquelin]

And if the $\sigma (r) = \sigma_ {0} * \ exp (- \frac {Rt} {L}) * (1 + (Rt-r) / SCL)$
The result will differ greatly?

In the function sigma(r), if you replace the exopential function (which tends to zero when r tends to infinity) by a linear function which tends to -infinity when r tends to infinity), indeed, the result will differ greatly.
So greatly that the integral (from 0 to infinity) is no longer convergent.

 

[Astaroth.]

In the function sigma(r), if you replace the exopential function (which tends to zero when r tends to infinity) by a linear function which tends to -infinity when r tends to infinity), indeed, the result will differ greatly.
So greatly that the integral (from 0 to infinity) is no longer convergent.

What do I do?

The exponential law of density distribution $\sigma (r)) = \sigma_{0} \exp(-\frac{r}{L})$
I want to apply a linear truncation for $\sigma (r)$
$\sigma (r) = \left\{\begin{matrix}\sigma (r), &r < Rt \\ \sigma (Rt)(1+(Rt-r)/SCL), & Rt < r < Rt+SCL\\ 0, & r > Rt+SCL \end{matrix}\right.$

 

[JJacquelin]

What do I do?

The exponential law of density distribution $\sigma (r)) = \sigma_{0} \exp(-\frac{r}{L})$
I want to apply a linear truncation for $\sigma (r)$
https://www.physicsforums.com/attachments/41402

OK, I understand : the linear function is truncated, which is very different regarding the Hankel integral.
Bur I cannot read the attachment : "Invalid Attachment specified"

 

[Astaroth.]

$\sigma (r) = \left\{\begin{matrix}\sigma (r), &r < Rt \\ \sigma (Rt)(1+(Rt-r)/SCL), & Rt < r < Rt+SCL\\ 0, & r > Rt+SCL \end{matrix}\right.$

 

[JJacquelin]

Well, I am afraid, this will be more complicated than with the previous sigma(r).
At first sight, solving analytically the integal S(k) seems possible.
Then, about the other integral V(R), I don't know yel. Now, I have not enough time available.

 

[Astaroth.]

Only you can help me.

 

[JJacquelin]

After more study in the case of the truncated law for sigma(r), I come to a conclusion :
Using the background provided by the Hankel transforms is no longer possible. We have to split the integral in two, each one on a limited range of integration. The background is less extended than in case of integration from zero to infinity.
Nevertheless, the integral S(k) can be analytically solved. In fact, it can be expressed in terms of a series of hypergeometric functions (this is of few interest for numerical calculus, since computing a lot of hypergeometric functions is not avantageous compare to a direct numerical integration).
Then, the other integral V(R) becommes very complicated, involving the product of hypergeometric functions and the Bessel function. I don't think that it could be analytically solved in present state of knowledge.
As a conclusion I suggest, if possible, to avoid the trucaded law of distribution : In is much simpler to apply the analytical solution found in case of the untruncated law.
If the truncated law is essential, my opinion is that there in no other way than the numerical computation of the integrals.
Sorry, that all I can do to help you concerning the particular case of truncated law of distribution.

 

[Astaroth.]

Thank you very much.