Can Ceva's Theorem Solve the Triangle Concurrency in POTW #329?

[Greg]

Hi everybody! :D I'll be filling in for anemone for about four weeks. I look forward to your participation in the upcoming POTWs.

Here is this week's POTW:

-----
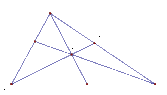
Consider the following triangle:
https://www.physicsforums.com/attachments/8353._xfImport

Show that the segments $AX$, $BY$, and $CZ$ are concurrent at $P$ if and only if $\frac{AZ}{BZ}\frac{BX}{CX}\frac{CY}{AY}=1$.-----

Remember to read the https://mathhelpboards.com/showthread.php?772-Problem-of-the-Week-%28POTW%29-Procedure-and-Guidelines to find out how to https://mathhelpboards.com/forms.php?do=form&fid=2!

 

[Greg]

Congratulations to kaliprasad for his correct solution which you can find below. :D

[sp] First let us prove one side that is equation holds if they are concurrent

Because AZ and BZ are the same base line so height to P is same using standard notation $\triangle$ for area

so $\frac{AZ}{BZ} = \frac{\triangle AZP}{\triangle BZP}$

again taking C we get

$\frac{AZ}{BZ} = \frac{\triangle AZC}{\triangle BZC}$

using law of proportion(below) and from above

$\frac{a}{b} = \frac{c}{d} = \frac{e}{f} = \frac{c-e}{d-f}$

we get

$\frac{AZ}{BZ} = \frac{\triangle AZC - \triangle AZP}{\triangle BZC- \triangle BZP} = \frac{\triangle ACP}{\triangle BCP}$

i. e

$\frac{AZ}{BZ} = \frac{\triangle ACP}{\triangle BCP}\cdots(1) $

similarly

$\frac{BX}{CX} = \frac{\triangle BAP}{\triangle ACP}\cdots(2) $

and

$\frac{CY}{AY} = \frac{\triangle BCP}{\triangle BAP}\cdots(3) $

multiplying (1), (2), (3) we get the result.

Now let us prove the otherway. that is the ratio holds.

Let us assume that CZ does not pass though P.

let CP intersect AB at Z'

now given $\frac{AZ}{BZ}\frac{BX}{CX}\frac{CY}{AY}= 1\cdots(4)$

as CP intersects AB at Z'

$\frac{AZ'}{BZ'}\frac{BX}{CX}\frac{CY}{AY}= 1\cdots(5)$

from (4) and (5) we get

$\frac{AZ}{BZ}=\frac{AZ'}{BZ'}$

or $\frac{AZ}{BZ}+1 =\frac{AZ'}{BZ'}+1$

or $\frac{AZ+ZB}{BZ}=\frac{AZ'+Z'B}{BZ'}$

or $\frac{AB}{BZ}=\frac{AB}{BZ'}$

or BZ=BZ' so Z = Z' and hence CZ passes through P hence proved[/sp]

A brief note regarding this weeks problem:

[sp]This result is known as Ceva's theorem.[/sp]