- #1
- 1,591
- 3
Don't wish to double-post, but last week or so, someone asked a question I've worked on and I was unable to find the thread:
Solve:
[tex]x^{Sin(y)}=y^{Cos(x)}[/tex]
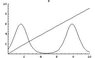
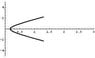
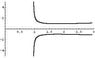
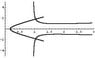
I've attached a plot of the solution for the first quadrant. Surprising isn't it? The only way I could do this is to brute-force check each point in the plane and choose it if close enough (<0.01) to make the expression zero. I can see no other way to do this.
Also, it becomes interesting when negative values are considered since the trig expressions return almost all irrational numbers and a negative number raised to an irrational number is not Real. Right?
There is a nice explanation for the form of the plot below. Note how the behavior changes as one moves up the y-axis: from curve to eye-shaped, to x-shaped, to inequality-shaped. Anyway, if you guys wish, I'll delete this post and link my comments to the original one if you tell me where it is.
Solve:
[tex]x^{Sin(y)}=y^{Cos(x)}[/tex]
I've attached a plot of the solution for the first quadrant. Surprising isn't it? The only way I could do this is to brute-force check each point in the plane and choose it if close enough (<0.01) to make the expression zero. I can see no other way to do this.
Also, it becomes interesting when negative values are considered since the trig expressions return almost all irrational numbers and a negative number raised to an irrational number is not Real. Right?
There is a nice explanation for the form of the plot below. Note how the behavior changes as one moves up the y-axis: from curve to eye-shaped, to x-shaped, to inequality-shaped. Anyway, if you guys wish, I'll delete this post and link my comments to the original one if you tell me where it is.
Attachments
Last edited: