Can diffusion be modelled as one-dimensional in this problem?

[Dario56]

I have a discussion with a colleague of mine.

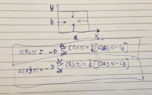
We have a thin cuboid sample whose two dimensions are similar to each other and are both much bigger than the sample thickness. I'm doing an experiment in which the diffusion of some species is induced and its diffusion profile is measured in one of the sample directions. Diffusion profile is fitted to the solutions of the diffusion equation (Fick's 2nd law) to obtain material properties.

Since the two dimensions of the sample are similar and I'm only measuring the diffusion profile in one of these two directions, is it meaningful to fit this profile to the one-dimensional diffusion equation solution? If you ask me, the answer is no. My colleague claims this can be done.

The problem is that the diffusion rate (molar flux) is similar in both dimensions (directions) and therefore concentration time change at any point is affected by the fluxes in both directions. Hence, we must measure the concentration profile over the sample surface and fit it to the two-dimensional solution.

Who do you think is right here? Can diffusion be modelled as one-dimensional?

 

[Chestermiller]

What is the exact physical situation? What are the boundary conditions? Is the diffusing species a trace species, of does it have a substantial concentration compared to the solvent?

 

[Dario56]

What is the exact physical situation? What are the boundary conditions? Is the diffusing species a trace species, of does it have a substantial concentration compared to the solvent?

Small solid sample. Diffusing species are oxide-ions created by oxygen reduction reaction on the gas/solid interphase. In that sense, it's a tracer.

Boundary conditions are of Dirchlect type. Concentration of the tracer isn't directly defined at the gas/solid interphase, but its molar flux. It's directly proportional to the difference of concentration at time $t$ and equilibrium concentration: $$ N(0,y,t) = -D \frac {\partial c(0,y,t)}{\partial x} = k (c(0,y,t) - c(eq))$$

$k$ is the measure of the oxygen reduction reaction rate on this material.

 

[Chestermiller]

Initial condition?

 

[Dario56]

Initial condition?

There is a known initial concentration of the tracer which is the same anywhere inside the sample before diffusion starts $$ c(x,y,0) = c_0 $$

 

[Chestermiller]

What you have described is a 2D diffusion problem. Concentration will be a function of 2 coordinates. If the outer boundary were circular concentration could be described by a single radial coordinate, and the problem would be 1D.

 

[Dario56]

What you have described is a 2D diffusion problem. Concentration will be a function of 2 coordinates. If the outer boundary were circular concentration could be described by a single radial coordinate, and the problem would be 1D.

Yes, that's what I think also. However, diffusion profile is measured along one of the coordinates. Therefore, one of the coordinates is kept constant and diffusion is effectively modelled as 1D although 2D solution must be used. What confuses me a bit here is that the value of constant coordinate (let's say $y$) will depend on the choice of the origin of the coordinate system and that seems to affect the concentration calculated from the model (and it shouldn't matter where we put the origin).

For example, if the sample has a surface of 5x4 (mm) and diffusion profile is measured along the y-coordinate 1mm from the the top than y-coordinate can be 1mm or 3mm depending on what sample edge we place the coordinate system origin. It would seem that plugging different y-coordinate values in the same solution of the diffusion equation would give a different result.

In circular samples, yes. Provided that the thickness is much smaller than the diameter.

 

[Chestermiller]

Yes, that's what I think also. However, diffusion profile is measured along one of the coordinates. Therefore, one of the coordinates is kept constant and diffusion is effectively modelled as 1D although 2D solution must be used. What confuses me a bit here is that the value of constant coordinate (let's say $y$) will depend on the choice of the origin of the coordinate system and that seems to affect the concentration calculated from the model (and it shouldn't matter where we put the origin).

For example, if the sample has a surface of 5x4 (mm) and diffusion profile is measured along the y-coordinate 1mm from the the top than y-coordinate can be 1mm or 3mm depending on what sample edge we place the coordinate system origin. It would seem that plugging different y-coordinate values in the same solution of the diffusion equation would give a different result.

This is not correct. The symmetry of the system will take care of this.

 

[Dario56]

This is not correct. The symmetry of the system will take care of this.

I'm not sure I understand this. The problem is I can't find the analytical solution for the 2D diffusion for my initial and boundary conditions.

Also, I realized I made a mistake earlier in boundary conditions. Here, I'll outline all initial and boundary conditions.

Initial condition is the same everywhere on the plane, some value of concentration: $$c(x,y,0) = c_0$$ Physically, this would be a background concentration of the tracer inside the sample.

Boundary conditions:

In the middle of the plane, $(x = \frac {a}{2},y = \frac {a}{2})$, concentration remains constant through the whole process. It's time independent and equal to the background tracer concentration. In another words, diffusion fronts from the opposite sample faces don't overlap. $$ u(\frac {a}{2},\frac {b}{2},t) = c_0 $$

On the plane boundaries, Dirichlet boundary conditions are imposed. Concentration isn't defined directly on the plane boundary, but the mole flux of the diffusing component: $$ N(0,y,t) = -D\nabla c(0,y,t) = k[c(0,y,t) - c_g] $$ and $$ N(x,0,t) = -D\nabla c(x,0,t) = k[c(x,0,t) - c_g] $$

Essentially, it's assumed that the mole flux on the boundary is directly proportional to the concentration difference between the component on the boundary and outside of it, $c_g$. Physically, this can be understood as the component existing in the gas phase with concentration $c_g$and entering a solid plane via some physicochemical process. Concentration, $c_g$ can also be defined as the equilibrium concentration on the plane when concentration gradient ceases at all points of the sample, $t \rightarrow \infty$.

 

[Chestermiller]

I'm not sure I understand this. The problem is I can't find the analytical solution for the 2D diffusion for my initial and boundary conditions.

I'm sure the solution exists for the analogous transient heat conduction problem. See Heat Transfer by Max Jacob.

Also, I realized I made a mistake earlier in boundary conditions. Here, I'll outline all initial and boundary conditions.

Initial condition is the same everywhere on the plane, some value of concentration: $$c(x,y,0) = c_0$$ Physically, this would be a background concentration of the tracer inside the sample.

This is OK

Boundary conditions:

In the middle of the plane, $(x = \frac {a}{2},y = \frac {a}{2})$, concentration remains constant through the whole process. It's time independent and equal to the background tracer concentration. In another words, diffusion fronts from the opposite sample faces don't overlap. $$ u(\frac {a}{2},\frac {b}{2},t) = c_0 $$

This makes no sense to me. Please provide a sketch (diagram) in the x-y plane. Also, it makes no sense to say that somewhere within the body, the concentration is constant, since, at long times, the concentration must approach ##c_g# everywhere within the domain.

On the plane boundaries, Dirichlet boundary conditions are imposed. Concentration isn't defined directly on the plane boundary, but the mole flux of the diffusing component: $$ N(0,y,t) = -D\nabla c(0,y,t) = k[c(0,y,t) - c_g] $$ and $$ N(x,0,t) = -D\nabla c(x,0,t) = k[c(x,0,t) - c_g] $$

Essentially, it's assumed that the mole flux on the boundary is directly proportional to the concentration difference between the component on the boundary and outside of it, $c_g$. Physically, this can be understood as the component existing in the gas phase with concentration $c_g$and entering a solid plane via some physicochemical process. Concentration, $c_g$ can also be defined as the equilibrium concentration on the plane when concentration gradient ceases at all points of the sample, $t \rightarrow \infty$.

The concentration gradient is a vector, while the right-hand side of your equation is a scalar. The correct boundary condition involves the normal component of the concentration gradient.

 

[Dario56]

I'm sure the solution exists for the analogous transient heat conduction problem. See Heat Transfer by Max Jacob.

I'll check it out. Thank you.

This makes no sense to me. Please provide a sketch (diagram) in the x-y plane. Also, it makes no sense to say that somewhere within the body, the concentration is constant, since, at long times, the concentration must approach ##c_g# everywhere within the domain.

Well, I think it means that the diffusion front doesn't reach the centre of the sample during the time frame of the process. Concentration gradient at that point remains zero inside the concerned time frame. If the time is long enough, diffusion front will reach the sample centre and concentration at that point will start to change. It could easily be I'm looking at this incorrectly.

Maybe as soon as non-stationary diffusion starts, mole flux is non-zero at every point in the sample.

The concentration gradient is a vector, while the right-hand side of your equation is a scalar. The correct boundary condition involves the normal component of the concentration gradient.

Yes, that's a mistake. Shouldn't it be a value of gradient at the point concerned, $|\nabla c(x,y,t)|$?

 

[Chestermiller]

I'll check it out. Thank you.

Well, I think it means that the diffusion front doesn't reach the centre of the sample during the time frame of the process. Concentration gradient at that point remains zero inside the concerned time frame. If the time is long enough, diffusion front will reach the sample centre and concentration at that point will start to change. It could easily be I'm looking at this incorrectly.

You have mass flowing into the plane but not out. So the latter interpretation is correct, and the concentration at these boundaries will change until they too ultimately reach $c_g$.

Yes, that's a mistake. Shouldn't it be a value of gradient at the point concerned, $|\nabla c(x,y,t)|$?

No. the tangential component of diffusion flux vector at a boundary results in no mass crossing the boundary. Only the component normal to the boundary results in mass diffusing across the boundary.

 

[Dario56]

You have mass flowing into the plane but not out. So the latter interpretation is correct, and the concentration at these boundaries will change until they too ultimately reach $c_g$.

The sketch is provided.

There is a flux across all 4 sides. Mole flux is in the opposite direction across the mutually parallel sides. It's something to include in the boundary conditions.

No. the tangential component of diffusion flux vector at a boundary results in no mass crossing the boundary. Only the component normal to the boundary results in mass diffusing across the boundary.

It's true that only normal component contributes to molar flow across the boundary. The problem I had is that $k(c - c_g)$ expression silently assumes normal component of the mole flux while that isn't explicitly written in the sources I've read. I thought molar flux in general is defined on the boundary.

 

[Dario56]

You have mass flowing into the plane but not out. So the latter interpretation is correct, and the concentration at these boundaries will change until they too ultimately reach $c_g$.

Hmm, it seems I've got some things to think about. In this problem, as it can be seen on the image provided, component diffuses through all 4 faces of the plane. I thought that concentration change in the sample centre can't change before the component coming from the plane edge arrives at that point. As component (oxide ion in my case) diffuses with finite velocity, it takes time for it to reach the centre. In another words, how can concentration change in the centre before any molar flux is present there? If there is no molar flux, how can its divergence be non-zero value?

 

[Chestermiller]

The sketch is provided. View attachment 339991
There is a flux across all 4 sides. Mole flux is in the opposite direction across the mutually parallel sides. It's something to include in the boundary conditions.

It's true that only normal component contributes to molar flow across the boundary. The problem I had is that $k(c - c_g)$ expression silently assumes normal component of the mole flux while that isn't explicitly written in the sources I've read. I thought molar flux in general is defined on the boundary.

No. $k(c-c_g)$ is the molar flux away from the boundary in the direction normal to the boundary. Neither flux vector nor magnitude of the flux vector is continuous at the boundary between the two media. Only normal flux components in the media on the two sides of the boundary are continuous.

Let me guess. You're a mathematician, and not a chemical engineer.

 

[Chestermiller]

Hmm, it seems I've got some things to think about. In this problem, as it can be seen on the image provided, component diffuses through all 4 faces of the plane. I thought that concentration change in the sample centre can't change before the component coming from the plane edge arrives at that point. As component (oxide ion in my case) diffuses with finite velocity, it takes time for it to reach the centre. In another words, how can concentration change in the centre before any molar flux is present there? If there is no molar flux, how can its divergence be non-zero value?

How can it not rise if values immediately adjacent to it do rise? You can't have a single point that is lower than all the surrounding points. Examine the finite difference approximation equation for elements with an edge along the boundary.

 

[Dario56]

No. $k(c-c_g)$ is the molar flux away from the boundary in the direction normal to the boundary.

Yes, I've already understood it from your previous response and that makes more sense. I was describing what was confusing me earlier.

Neither flux vector nor magnitude of the flux vector is continuous at the boundary between the two media. Only normal flux components in the media on the two sides of the boundary are continuous.

Let me guess. You're a mathematician, and not a chemical engineer.

Not often I can see this to you (as I learned a lot from our discussions here), but your assumption is incorrect. I'm a chemical engineer.

 

[Chestermiller]

Yes, I've already understood it from your previous response and that makes more sense. I was describing what was confusing me earlier.

Not often I can see this to you (as I learned a lot from our discussions here), but your assumption is incorrect. I'm a chemical engineer.

Excellent. So, have you ever work with Transport Phenomena by Bird, Stewart, and Lightfoot. During my long career at DuPont, I used this book more than all the others combined. it is a gem.

 

[Dario56]

How can it not rise if values immediately adjacent to it do rise? You can't have a single point that is lower than all the surrounding points. Examine the finite difference approximation equation for elements with an edge along the boundary.

I think I don't have accurate picture of the diffusion process. When I think about the simulations of the non-stationary diffusion in Matlab for example (finite difference numerical solution), I remember how time change in concentration happens simultaneously at all points and concentration gradient also decreases continuously. Diffusion profile becomes flater and flater.

You can't have a single point that is lower than all the surrounding points.

However, when I think about the process in the head, I think about it as the component diffusing from the edge inwards. My picture in the head is that the surrounding points aren't higher before component diffusing from the gas phase into the sample comes to these points. Points around it aren't higher before enough time has passed for diffusion to reach these points. It's a process happening in series not parallel where component diffuses from point to point following the concentration gradient. Mole flux and concentration gradient are vectors and therefore defined at the point. Component only knows what is happening at the point and follows the vector field of molar flux from point to point. As the time goes, diffusion progresses deeper and deeper into the sample (diffusion length goes up).

It seems that this picture is incorrect and process actually happens in parallel, simultaneously at all points. What isn't intuitive to me is how can concentration gradient field come into existence immediately at all points? Drawing a parallel with electrostatics can be done where electric field is defined at every point as soon as we apply potential difference between two points. Molar flux is replaced by current density and concentration gradient with electric field. We can think of concentration gradient as some kind of ''chemical'' force field (analogous to electric field - electric force relationship) creating a molar flux (current density).

However, there is no force here in reality and that's the reason why the analogy with electrostatics doesn't actually work. It's just statistics and probability theory applied to the large collection of randomly moving particles. In electrostatics, electric force acts on charges creating current density. This force (and therefore electric field) decreases with the distance squared (inverse square law). There is no any such force in diffusion acting on particles and creating molar flux. In that sense, if the concentration gradients don't exist initially inside the sample, how can they suddenly come into existence everywhere when diffusion starts? Diffusion molar fluxes don't arise from interaction unlike electric currents created by electric fields. My picture is that they need to be created at some points and then propagate through space as time goes.

As there is no force here, diffusion should propagate point to point, following the concentration gradient field. In another words, process happens in series, not parallel.

 

[Dario56]

Excellent. So, have you ever work with Transport Phenomena by Bird, Stewart, and Lightfoot. During my long career at DuPont, I used this book more than all the others combined. it is a gem.

I did, classic textbook. The start of the new paradigm in ChemE.

 

[Dario56]

Excellent. So, have you ever work with Transport Phenomena by Bird, Stewart, and Lightfoot. During my long career at DuPont, I used this book more than all the others combined. it is a gem.

After discussing the question from the last comment, I learned that diffusion equation being the parabolic PDE does one approximation which answers my previous question. Namely, that any perturbation from equilibrium (in my case, mole flux being imposed on the boundary) is propagated with infinite speed through the body. In another words, concentration gradient imposed on the boundary instantaneously travels to every point of the sample. That's an implicit assumption of the parabolic PDEs and for most practical problems, very good approximation as perturbations in general travel very fast compared to the sample or system dimensions. In the fraction of the second, perturbation is the same everywhere.

It's something similar how electric fields being propagated at the speed of light poses no measurable time delays in any electrical circuit components. Speed of light is just too big compared to the dimensions of electrical circuits.