- #1
FXpilot
- 2
- 0
So the problem is asking me to derive the centrifugal and coriolis accelerations of the moon when it is furthest from the Sun and when it is orthogonal to the radius between Earth and the Sun.
Given:
Radius of Moon's Orbit around Earth
Radius of Earth's Orbit around Sun
Mass of Earth
Mass of Sun
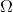 = Angular Frequency of the revolution of the Earth around the Sun
= Angular Frequency of the revolution of the Earth around the Sun
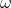 = Angular Frequency of the Revolution of the Moon around the Earth
= Angular Frequency of the Revolution of the Moon around the Earth
I am trying to figure out the first part.
I know that the coriolis acceleration is going to be zero when the moon is furthest from the Sun because the velocity of the moon is parallel to the angular frequency of the trajectory of the Earth Moon system around the sun.
I already derived that the centrifugal acceleration that the moon experiences by the Earth is
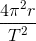
T being the period of the moon around the Earth So would the total centrifugal acceleration that the Moon experiences be the :
Centrifugal Acceleration of the moon by Earth + Centrifugal Acceleration of the moon by Sun?
So
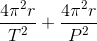
P being the period of the Earth moon system around the sun
Thanks
Given:
Radius of Moon's Orbit around Earth
Radius of Earth's Orbit around Sun
Mass of Earth
Mass of Sun
I am trying to figure out the first part.
I know that the coriolis acceleration is going to be zero when the moon is furthest from the Sun because the velocity of the moon is parallel to the angular frequency of the trajectory of the Earth Moon system around the sun.
I already derived that the centrifugal acceleration that the moon experiences by the Earth is
T being the period of the moon around the Earth So would the total centrifugal acceleration that the Moon experiences be the :
Centrifugal Acceleration of the moon by Earth + Centrifugal Acceleration of the moon by Sun?
So
P being the period of the Earth moon system around the sun
Thanks