Lotto
- 251
- 16
Thread moved from the technical forums to the schoolwork forums
TL;DR Summary: I have to find an equivalent resistance of the circuit below, dependent on the amount of ##R_3## - resistors.
Here is the circuit:
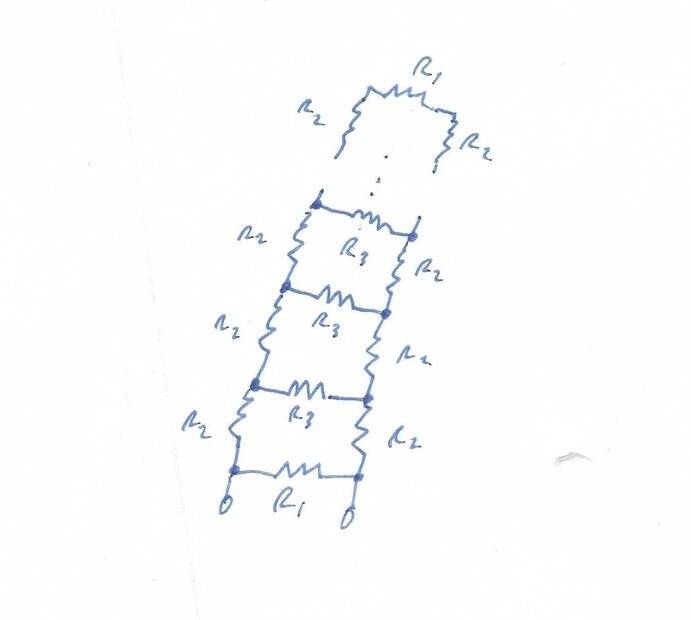
I think there is no general solution. When I want to calculate it, I have to do ##((((R_1+2R_2)^{-1}+{R_3}^{-1})^{-1}+2R_2)^{-1}+{R_3}^{-1})^{-1}...##, so it is kind of crazy. Is there any general solution dependent on the amount of ##R_3## - resistors ##n##? So something like ##R_{\mathrm {eq} _n}=....##.
Here is the circuit:
I think there is no general solution. When I want to calculate it, I have to do ##((((R_1+2R_2)^{-1}+{R_3}^{-1})^{-1}+2R_2)^{-1}+{R_3}^{-1})^{-1}...##, so it is kind of crazy. Is there any general solution dependent on the amount of ##R_3## - resistors ##n##? So something like ##R_{\mathrm {eq} _n}=....##.