Can Logarithms Be Used to Solve a Tricky Exponential Problem?

[chwala]

Homework Statement

see attached.

Relevant Equations

logs

Find question here;

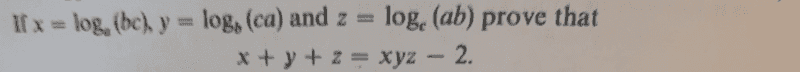See my attempt;
$$a^x=bc$$
$$(a^x)^{yz} = (bc)^{yz}$$
$$a^{xyz} = (b^y)^z (c^z)^y $$
$$a^{xyz} = (ac)^z (ab)^y $$
$$a^{xyz} = a^z c^z a^y b^y$$
$$a^{xyz} = a^z(ab)a^y(ac)$$
$$a^{xyz} = a^2(bc) a^{y+z}$$
$$a^{xyz} = a^{y+z+2} (bc)$$
$$a^{xyz} = a^{y+z+2} a^x$$
$$a^{xyz} = a^{x+y+z+2} $$ bingo!

I would be interested in the proof by use of logarithms...i tried this and i was going round in circles...but i should be able to do it! I guess the hint here would be to express all the logs to base $a$...I will check this out later. Meanwhile, any other approach is welcome...time now for a deserved cake and coffee...

 

[Sunay_]

If $x = \log_{a}{bc}$

Then $x+1 = \log_{a}{bc} + \log_{a}{a} = \log_{a}{abc}$

We can equate all the arguments in this way namely abc and then turn it into base by taking reverses.

So,

$\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1} = 1$ and this gives the desired equality.

 

[chwala]

If $x = \log_{a}{bc}$

Then $x+1 = \log_{a}{bc} + \log_{a}{a} = \log_{a}{abc}$

We can equate all the arguments in this way namely abc and then turn it into base by taking reverses.

So,

$\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1} = 1$ and this gives the desired equality.

Looks interesting...I'll look at this later...thanks.

 

[chwala]

This part;
$x+1 = \log_{a}{bc} + \log_{a}{a} = \log_{a}{abc}$ is clear. Am trying to understand the next part of your working...i do not seem to get it...

 

[chwala]

Ok, since they want us to prove( to show that lhs = rhs of equation) that,

$$x+y+z=xyz-2$$
$$⇒x+y+z+2=xyz$$...i will now try to prove that the lhs= rhs.
$$\log_a(bc)+\log_b(ac)+\log_c(ab)+2= (\log_a(bc))(\log_b(ac))(\log_c(ab))$$
Consider the lhs of the equation, it follows that;
$$\log_ab+\log_ac+\log_ba+\log_bc+\log_ca+log_cb$$
$$⇒(m+\frac {1}{d}+\frac {1}{m}+q+d+\frac {1}{q})+2$$
$$=m+q+d+\frac {1}{m}+\frac {1}{q}+\frac {1}{d}+2$$

Now, consider the rhs of the equation,
$$(\log_a(bc))(\log_b(ac))(\log_c(ab))= (m+\frac {1}{d})(q+\frac {1}{m})(d+\frac {1}{q})$$
$$=mqd+m+d+\frac {1}{q}+q+ \frac {1}{d}+ \frac {1}{m}+ \frac {1}{qmd}$$
$$=m+q+d+\frac {1}{m}+\frac {1}{q}+\frac {1}{d}+mqd+ \frac {1}{qmd}$$

Now to deal with,
$$mqd+ \frac {1}{qmd}$$, note that,
$$mqd=(\log_ab)(\log_bc)(log_ca)=\log_ab \frac {\log_ac}{\log_ab}\frac {\log_aa}{\log_ac}=1$$
therefore,
$$mqd+ \frac {1}{qmd}=1+\frac{1}{1}=2$$
thus proved. Cheers guys

 

[Sunay_]

This part;
$x+1 = \log_{a}{bc} + \log_{a}{a} = \log_{a}{abc}$ is clear. Am trying to understand the next part of your working...i do not seem to get it...

I tried to imply that if $x+1 = \log_{a}{abc}$ then $\frac{1}{x+1} = \log_{abc}{a}$

The same is true for $\log_{abc}{b}$ and $\log_{abc}{c}$

So, because $\log_{abc}{a}+\log_{abc}{b}+\log_{abc}{c}=\log_{abc}{abc}=1$ is true,

The solution can be found using this:

$\frac{1}{x+1}+\frac{1}{y+1}+\frac{1}{z+1} = 1$ and this gives the desired equality.

I hope I could be of help.