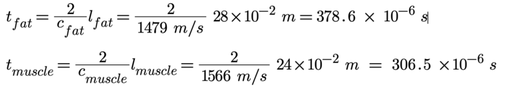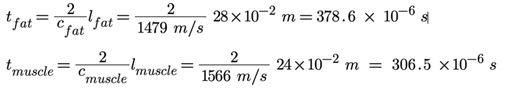Can Multiple Reflections Be Eliminated Using A-Mode Imaging in Ultrasound?

[nao113]

Homework Statement

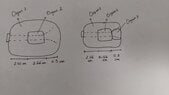
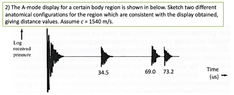
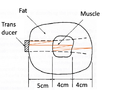
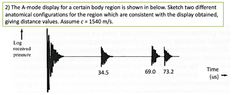
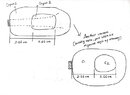
(a) For the anatomical configuration shown right, sketch the arrival times of all echoes as they would be seen on an A-mode display. Do not calculate echo strengths, merely calculate times of arrival referenced to the initial transmit time, out to a maximum of 200 us. Include multiple reflections and use the precise phase velocity of the materials shown.
(b) What percentage error is introduced in the calculated arrival time of the first echo if the velocity is assumed to be the average calibration value (c = 1540 m/s) rather than fat?

Relevant Equations

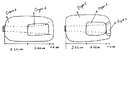
t1 = (2/c1) l1
t2 =t1+(2/c2) l2

Here is my answer:
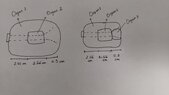
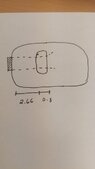
PART A:

Those three didn't surpass 200 us.
But, I am still wondering whether I did it right or not since I don t really understand the meaning of `multiple reflections `. I don't know whether I have answered for multiple reflections in my answer above. or should I double the value t1, or t2 to include multiple reflections.

The picture above is the sample in the material, but I still don't understand.

PART B:

Please help me to point out my mistake in the answers. Thank you

 

[TSny]

Your calculations look good so far.

Multiple reflections occur when there is more than one reflection before the sound is detected. Here are some examples:

The two pictures on the left have three reflections. The picture on the right has five reflections. Clearly, there are many possibilities. Fortunately, you only need to be concerned with cases for which the total travel time is less than 200 μs.

So far, you have found 3 cases with travel times less than 200 μs. These are single reflection cases. Can you find any cases of multiple reflections where the total travel time is less than 200 μs?

 

[nao113]

Your calculations look good so far.

Multiple reflections occur when there is more than one reflection before the sound is detected. Here are some examples:

View attachment 301422
The two pictures on the left have three reflections. The picture on the right has five reflections. Clearly, there are many possibilities. Fortunately, you only need to be concerned with cases for which the total travel time is less than 200 μs.

So far, you have found 3 cases with travel times less than 200 μs. These are single reflection cases. Can you find any cases of multiple reflections where the total travel time is less than 200 μs?

Thank you very much for the explanation, okay, I ll try to do it. Btw, for part b about the error, did you think I get it right?

 

[TSny]

Btw, for part b about the error, did you think I get it right?

Yes, it looks right.

 

[nao113]

Your calculations look good so far.

Multiple reflections occur when there is more than one reflection before the sound is detected. Here are some examples:

View attachment 301422
The two pictures on the left have three reflections. The picture on the right has five reflections. Clearly, there are many possibilities. Fortunately, you only need to be concerned with cases for which the total travel time is less than 200 μs.

So far, you have found 3 cases with travel times less than 200 μs. These are single reflection cases. Can you find any cases of multiple reflections where the total travel time is less than 200 μs?

Your calculations look good so far.

Multiple reflections occur when there is more than one reflection before the sound is detected. Here are some examples:

View attachment 301422
The two pictures on the left have three reflections. The picture on the right has five reflections. Clearly, there are many possibilities. Fortunately, you only need to be concerned with cases for which the total travel time is less than 200 μs.

So far, you have found 3 cases with travel times less than 200 μs. These are single reflection cases. Can you find any cases of multiple reflections where the total travel time is less than 200 μs?

Hello, related to the statement `Do not calculate echo strengths, merely calculate times of arrival referenced to the initial transmit time, out to a maximum of 200 us.“ What does it actually mean?

honestly, I am confused about what “t“ means? is it the variable for each echo?

I tried to calculate based on the picture I sent. I think this one is multiple reflection with less than 200 us.
My answer is on the next post

 

[nao113]

 

[TSny]

Let's take your nice example:

We want to find the total time that it takes the sound to travel this complicated path. This will be the time at which the echo is detected for this multiple-reflection example.

Note that the sound travels four times through the 5 cm of fat on the left side, as shown below in blue:

The sound also travels twice through the 4 cm of fat on the right:

That makes a total distance of 28 cm of travel through fat.

The sound also travels six times through the 4 cm of muscle, as shown in green:

So that's 24 cm of travel through muscle.

How much time does it take the sound to travel through 28 cm of fat?
How much time does it take the sound to travel through 24 cm of muscle?
What's the time at which the echo for this example is detected?

 

[nao113]

Let's take your nice example:
View attachment 301596

We want to find the total time that it takes the sound to travel this complicated path. This will be the time at which the echo is detected for this multiple-reflection example.

Note that the sound travels four times through the 5 cm of fat on the left side, as shown below in blue:
View attachment 301597

The sound also travels twice through the 4 cm of fat on the right:
View attachment 301598

That makes a total distance of 28 cm of travel through fat.

The sound also travels six times through the 4 cm of muscle, as shown in green:

View attachment 301599
So that's 24 cm of travel through muscle.

How much time does it take the sound to travel through 28 cm of fat?
How much time does it take the sound to travel through 24 cm of muscle?
What's the time at which the echo for this example is detected?

Thank you very much for the guidance, I calculated the question you asked. btw, I didn't know how to calculate “What's the time at which the echo for this example is detected?“ Do I just need to do addition as 378.6 us + 306.5 us = 658.1 us for ur third ? Which one that I need to get less than 200 us? Is it your 1 and 2 questions or the third one? Thank youuu

 

[TSny]

Thank you very much for the guidance, I calculated the question you asked. btw, I didn't know how to calculate “What's the time at which the echo for this example is detected?“ Do I just need to do addition as 378.6 us + 306.5 us = 658.1 us for ur third ?

Yes, you would add the total time traveled in the fat to the total time traveled in the muscle to get the time of arrival of the echo. But, I don't agree with your numbers 378.6 μs and 306.5 μs. These are twice what I get. Can you explain how you obtained these results?

Which one that I need to get less than 200 us? Is it your 1 and 2 questions or the third one? Thank youuu

It's the time of arrival of the echo (my third question) that needs to be less than 200 μs.

 

[nao113]

Yes, you would add the total time traveled in the fat to the total time traveled in the muscle to get the time of arrival of the echo. But, I don't agree with your numbers 378.6 μs and 306.5 μs. These are twice what I get. Can you explain how you obtained these results?It's the time of arrival of the echo (my third question) that needs to be less than 200 μs.

I explained how I got them in the picture I attached, is it visible on your side? May I know how you got ur answer?

 

[nao113]

Here it is

 

[Steve4Physics]

Hi @nao113. Some thoughts which might help.

You can save work by converting speeds to cm/μ s at the start. Then to get a time, you simply divide distance (in cm) by the speed (in cm/μs).

E.g. $c_{muscle}$ = 1566m/s = 0.1566cm/μs.

The fastest speed is in muscle. The furthest distance which can be covered in 200 μs is therefore 200μs x 0.1566 cm/μ s = 31.32cm (less if there is some fat).

Paths longer than 31.23cm will take more than 200μs and can be ignored.

We can represent the layers like this:

A←5cm fat→B←4cm muscle→C←4cm fat→D​

The simplest possible paths (one reflection each) are:
A→B→A (path-length= 5cm+5cm=10cm)
A→B→C→B→A(path-length= 5cm+4cm+ 4cm+5cm =18cm)
A→B→C→D→C→B-A(path-length=5cm+4cm+ 4cm+4cm + 4cm+5cm = =26cm)
So these explain three of the signals of the display

Many other paths are possible, e.g.
A→B→A→B→A (path-length= 5cm+5cm+5cm+5cm+ = 20cm

Think about the possible paths. You can ignore paths of length greater than 32.32cm. (Note that a path through a lot of fat, can be less than 32.32cm but still take more than 200μs; so these need separate checking.)

A few other points...

In the formula $t = (\frac 2 c)l$ note that $l$ is the depth and the factor 2 doubles it to give path-length. Don’t accidentally use $l$ as the path-length.

Be careful with your choice of symbols. In a post #1 attachment you used $c_1$ and $c_3$ for the speed in fat. You should use the same symbol for the same quantity..

And (even worse!) you wrote:
$\epsilon = \frac {t_1 – t_1}{t_1} \times 100%$
which (I hope you realize) gives zero!
You need different symbols for different times.

Make sure your understand what is going on – don’t just be plug numbers into formulae.

 

[TSny]

The total time of travel through the fat is just $$t_{fat} = \frac{\rm distance \,traveled \, through \, fat}{\rm speed \, through \, fat}$$
We found that the distance through the fat is 28cm. So, the time of travel through the fat is $$t_{fat} = \frac{0.28 \rm m}{1479 \; \rm m/s}$$
You calculated this as $t_{fat} = 2 \frac{0.28 m}{1479 m/s}$. The factor of 2 should not be there.

I think you are maybe getting confused because of the way the textbook or class notes wrote $t_1 = \frac{2}{c_1} l_1$ for the case shown below

You can see that the distance traveled is $2 l_1$. So, the arrival time for the echo is $t_1 = \frac{2 l_1}{c_1}$. And this can be written as $t_1 = \frac{2}{c_1} l_1$.

[Edited to correct a typo]

 

[TSny]

And (even worse!) you wrote:
$\epsilon = \frac {t_1 – t_1}{t_1} \times 100%$
which (I hope you realize) gives zero!
You need different symbols for different times.

It's hard to see , but I think the OP has a prime on the second $t_1$ in the numerator:

 

[Steve4Physics]

It's hard to see , but I think the OP has a prime on the second $t_1$ in the numerator:
View attachment 301639

Thanks @TSny. You are correct. I should have looked more carefully (and should clean my screen more often). Apologies to @nao113 .

 

[nao113]

Thanks @TSny. You are correct. I should have looked more carefully (and should clean my screen more often). Apologies to @nao113 .

No worries, btw, thank you for your attention, you helped me a lot

 

[nao113]

The total time of travel through the fat is just $$t_{fat} = \frac{\rm distance \,traveled \, through \, fat}{\rm speed \, through \, fat}$$
We found that the distance through the fat is 28cm. So, the time of travel through the fat is $$t_{fat} = \frac{0.28 \rm m}{1479 \; \rm m/s}$$
You calculated this as $t_{fat} = 2 \frac{0.28 m}{1479 m/s}$. The factor of 2 should not be there.

I think you are maybe getting confused because of the way the textbook or class notes wrote $t_1 = \frac{2}{c_1} l_1$ for the case shown below
View attachment 301635

You can see that the distance traveled is $2 l_1$. So, the arrival time for the echo is $t_1 = \frac{2 l_1}{c_1}$. And this can be written as $t_1 = \frac{2}{c_1} l_1$.

[Edited to correct a typo]

I see I got it, I will try to implement your solution, that s a very complete explanation Thank you very much. Btw, may I have another question? These are the question and my answer. The question asked me to draw, did I draw it right?

 

[nao113]

Hi @nao113. Some thoughts which might help.

You can save work by converting speeds to cm/μ s at the start. Then to get a time, you simply divide distance (in cm) by the speed (in cm/μs).

E.g. $c_{muscle}$ = 1566m/s = 0.1566cm/μs.

The fastest speed is in muscle. The furthest distance which can be covered in 200 μs is therefore 200μs x 0.1566 cm/μ s = 31.32cm (less if there is some fat).

Paths longer than 31.23cm will take more than 200μs and can be ignored.

We can represent the layers like this:

A←5cm fat→B←4cm muscle→C←4cm fat→D​

The simplest possible paths (one reflection each) are:
A→B→A (path-length= 5cm+5cm=10cm)
A→B→C→B→A(path-length= 5cm+4cm+ 4cm+5cm =18cm)
A→B→C→D→C→B-A(path-length=5cm+4cm+ 4cm+4cm + 4cm+5cm = =26cm)
So these explain three of the signals of the display

Many other paths are possible, e.g.
A→B→A→B→A (path-length= 5cm+5cm+5cm+5cm+ = 20cm

Think about the possible paths. You can ignore paths of length greater than 32.32cm. (Note that a path through a lot of fat, can be less than 32.32cm but still take more than 200μs; so these need separate checking.)

A few other points...

In the formula $t = (\frac 2 c)l$ note that $l$ is the depth and the factor 2 doubles it to give path-length. Don’t accidentally use $l$ as the path-length.

Be careful with your choice of symbols. In a post #1 attachment you used $c_1$ and $c_3$ for the speed in fat. You should use the same symbol for the same quantity..

And (even worse!) you wrote:
$\epsilon = \frac {t_1 – t_1}{t_1} \times 100%$
which (I hope you realize) gives zero!
You need different symbols for different times.

Make sure your understand what is going on – don’t just be plug numbers into formulae.

Thank you very much for the explanation, this is so detail ... I ll try to use this understanding on my answer

 

[nao113]

Hi @nao113. Some thoughts which might help.

You can save work by converting speeds to cm/μ s at the start. Then to get a time, you simply divide distance (in cm) by the speed (in cm/μs).

E.g. $c_{muscle}$ = 1566m/s = 0.1566cm/μs.

The fastest speed is in muscle. The furthest distance which can be covered in 200 μs is therefore 200μs x 0.1566 cm/μ s = 31.32cm (less if there is some fat).

Paths longer than 31.23cm will take more than 200μs and can be ignored.

We can represent the layers like this:

A←5cm fat→B←4cm muscle→C←4cm fat→D​

The simplest possible paths (one reflection each) are:
A→B→A (path-length= 5cm+5cm=10cm)
A→B→C→B→A(path-length= 5cm+4cm+ 4cm+5cm =18cm)
A→B→C→D→C→B-A(path-length=5cm+4cm+ 4cm+4cm + 4cm+5cm = =26cm)
So these explain three of the signals of the display

Many other paths are possible, e.g.
A→B→A→B→A (path-length= 5cm+5cm+5cm+5cm+ = 20cm

Think about the possible paths. You can ignore paths of length greater than 32.32cm. (Note that a path through a lot of fat, can be less than 32.32cm but still take more than 200μs; so these need separate checking.)

A few other points...

In the formula $t = (\frac 2 c)l$ note that $l$ is the depth and the factor 2 doubles it to give path-length. Don’t accidentally use $l$ as the path-length.

Be careful with your choice of symbols. In a post #1 attachment you used $c_1$ and $c_3$ for the speed in fat. You should use the same symbol for the same quantity..

And (even worse!) you wrote:
$\epsilon = \frac {t_1 – t_1}{t_1} \times 100%$
which (I hope you realize) gives zero!
You need different symbols for different times.

Make sure your understand what is going on – don’t just be plug numbers into formulae.

the question asked me to include multiple reflections, so it doesn't mean I need to make three different path for the anatomical configuration, right? There are single reflection you mentioned:
A→B→A (path-length= 5cm+5cm=10cm)
A→B→C→B→A(path-length= 5cm+4cm+ 4cm+5cm =18cm)
A→B→C→D→C→B-A(path-length=5cm+4cm+ 4cm+4cm + 4cm+5cm = =26cm)

So, to create multiple reflection, I need to make a new path like A -> B -> A -> C -> A ( 5 + 5 + 5 + 4 + 4 + 5 = 28 cm) -> based on my calculation, it will produce less than 200 us. Am I correct?

 

[nao113]

Your calculations look good so far.

Multiple reflections occur when there is more than one reflection before the sound is detected. Here are some examples:

View attachment 301422
The two pictures on the left have three reflections. The picture on the right has five reflections. Clearly, there are many possibilities. Fortunately, you only need to be concerned with cases for which the total travel time is less than 200 μs.

So far, you have found 3 cases with travel times less than 200 μs. These are single reflection cases. Can you find any cases of multiple reflections where the total travel time is less than 200 μs?

Btw, for multiple reflection, can I stop on the muscle, let say there are A - B = 5 cm, B-C = 4 cm, and C-D= 4 cm. Can I stop on B? so it will be like A-B-A-C-B-D-C, can I do that?

 

[TSny]

the question asked me to include multiple reflections, so it doesn't mean I need to make three different path for the anatomical configuration, right?

I'm not quite sure what you are asking here.

There are single reflection you mentioned:
A→B→A (path-length= 5cm+5cm=10cm)
A→B→C→B→A(path-length= 5cm+4cm+ 4cm+5cm =18cm)
A→B→C→D→C→B-A(path-length=5cm+4cm+ 4cm+4cm + 4cm+5cm = =26cm)

Yes. Of course, for A→B→C→B→A you need to take into account that 10 cm of length takes place in fat and 8 cm takes place in muscle. It looks like you correctly calculated the time for this path in your first post.
A simple way to calculate this is $t_{\rm echo} = \frac{.10 \, \rm m}{1479 \, \rm m/s} +\frac{.08 \, \rm m}{1566 \, \rm m/s} = 118.7 \, \mu \rm s$

Likewise, for the path A→B→C→D→C→B-A you can see that 18 cm takes place in fat and 8 cm takes place In muscle. So,
$t_{\rm echo} = \frac{.18 \, \rm m}{1479 \, \rm m/s} +\frac{.08 \, \rm m}{1566 \, \rm m/s} = 172.8 \, \mu \rm s$. This agrees with what you got for this path in your first post.

So, to create multiple reflection, I need to make a new path like A -> B -> A -> C -> A ( 5 + 5 + 5 + 4 + 4 + 5 = 28 cm) -> based on my calculation, it will produce less than 200 us. Am I correct?

Yes, I also get less than 200 μs for this case. If you want to tell me the specific answer that you got for this case, I can tell you if I agree.

 

[TSny]

Btw, for multiple reflection, can I stop on the muscle, let say there are A - B = 5 cm, B-C = 4 cm, and C-D= 4 cm. Can I stop on B? so it will be like A-B-A-C-B-D-C, can I do that?

No. The sound must return to the transducer in order to be registered as an echo. So, all paths must start and end at A.

 

[nao113]

I'm not quite sure what you are asking here.Yes. Of course, for A→B→C→B→A you need to take into account that 10 cm of length takes place in fat and 8 cm takes place in muscle. It looks like you correctly calculated the time for this path in your first post.
A simple way to calculate this is $t_{\rm echo} = \frac{.10 \, \rm m}{1479 \, \rm m/s} +\frac{.08 \, \rm m}{1566 \, \rm m/s} = 118.7 \, \mu \rm s$

Likewise, for the path A→B→C→D→C→B-A you can see that 18 cm takes place in fat and 8 cm takes place In muscle. So,
$t_{\rm echo} = \frac{.18 \, \rm m}{1479 \, \rm m/s} +\frac{.08 \, \rm m}{1566 \, \rm m/s} = 172.8 \, \mu \rm s$. This agrees with what you got for this path in your first post.Yes, I also get less than 200 μs for this case. If you want to tell me the specific answer that you got for this case, I can tell you if I agree.

Thank you so much for the detail information. Okay, I ll share my full answer, btw, can I ask another question? I already answered it, here they are. Did I do it correctly?

 

[nao113]

I'm not quite sure what you are asking here.Yes. Of course, for A→B→C→B→A you need to take into account that 10 cm of length takes place in fat and 8 cm takes place in muscle. It looks like you correctly calculated the time for this path in your first post.
A simple way to calculate this is $t_{\rm echo} = \frac{.10 \, \rm m}{1479 \, \rm m/s} +\frac{.08 \, \rm m}{1566 \, \rm m/s} = 118.7 \, \mu \rm s$

Likewise, for the path A→B→C→D→C→B-A you can see that 18 cm takes place in fat and 8 cm takes place In muscle. So,
$t_{\rm echo} = \frac{.18 \, \rm m}{1479 \, \rm m/s} +\frac{.08 \, \rm m}{1566 \, \rm m/s} = 172.8 \, \mu \rm s$. This agrees with what you got for this path in your first post.Yes, I also get less than 200 μs for this case. If you want to tell me the specific answer that you got for this case, I can tell you if I agree.

Here is my full answer.. do you agree with me? Thank you

 

[TSny]

Thank you so much for the detail information. Okay, I ll share my full answer, btw, can I ask another question? I already answered it, here they are. Did I do it correctly?

Both of these configurations would produce the A-mode display of echos. But, the two configurations are esssentially the same since they both consist of two 2.66 cm regions and one 0.3 cm region and all three regions are assumed to have the same sound speed c. Can you come up with a different configuration that is fundamentally different and would produce the same display of echos?

 

[nao113]

View attachment 301664

Both of these configurations would produce the A-mode display of echos. But, the two configurations are esssentially the same since they both consist of two 2.66 cm regions and one 0.3 cm region and all three regions are assumed to have the same sound speed c. Can you come up with a different configuration that is fundamentally different and would produce the same display of echos?

How about I replaced the first picture with this one? so only 2 organs here with one 2.66 cm region and one 0.3 cm region. Then, should I name these two organs as organ 4 and organ 5? since organ 1, 2, and 3 are used in the second picture?, by doing that, it seems that they will have different speed of c

 

[TSny]

How about I replaced the first picture with this one?

This won't work since it would produce an echo at 38.4 μs which does not appear in the echo display diagram. Can you see how this echo would be produced?

 

[TSny]

By the way, in your figure shown below you might want to calculate the 0.3 cm distance more accurately so that it is accurate to the nearest 0.01 cm.

 

[nao113]

View attachment 301667
This won't work since it would produce an echo at 38.4 μs which does not appear in the echo display diagram. Can you see how this echo would be produced?

Yes, I just realized it will produced 38.4. is there any formula to recreate another anatomical configurations? Can you explain more about what should I have to do? Here, I tried another one, is it correct?

 

[nao113]

By the way, in your figure shown below you might want to calculate the 0.3 cm distance more accurately so that it is accurate to the nearest 0.01 cm.
View attachment 301666

Yes, I changed the way I draw it so the distance will look more realistic

 

[TSny]

Here is my full answer.. do you agree with me? Thank you

I agree with these. However, there is another case that you have missed.

 

[nao113]

I agree with these. However, there is another case that you have missed.

May I know what is it?

 

[TSny]

May I know what is it?

I don't want to give it away. It is not a very complicated path. Try playing around with various paths.

 

[TSny]

Yes, I just realized it will produced 38.4. is there any formula to recreate another anatomical configurations? Can you explain more about what should I have to do? Here, I tried another one, is it correct?

This will produce the echos at 34.5 μs and 69.0 μs. It will not produce the 73.2 μs echo unless the distance $l_3 = 0.32$ cm. But you already discovered that case.

What if you choose $l_2$ to be something other than 2.66 cm?
Can you choose it so that you get echos at 34.5 μs, 69.0 μs, and 73.2 μs and no other echos with arrival times less than about 75 μs?

 

[nao113]

I don't want to give it away. It is not a very complicated path. Try playing around with various paths.

Sure, I ll try to find other paths, thank you very much