- #1
goody1
- 16
- 0
Good evening! Could anybody help me with this limit?
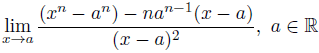
I have a problem when there are two variables. The only thing I did was that:
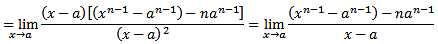 ,
,
but I don't know if it was helpful. Thank you!
I have a problem when there are two variables. The only thing I did was that:
but I don't know if it was helpful. Thank you!