genxium
- 137
- 2
- TL;DR Summary
- If n(number of slits) is around 1000, can we produce an intensity pattern whose adjacent local minimas are separated by a distance less than the wavelength of incident light?
According to the intensity formula
I = I_0 \cdot \frac{sin^2(n\phi/2)}{sin^2(\phi/2)}
(quoted from Feynman Lectures Vol I)
Therefore the 2 local minimas adjacent to each global maxima are angularly \Delta \phi_{localmin} = \frac{4\pi}{n} apart. When trying to think of a use case to exploit this formula I got something like this
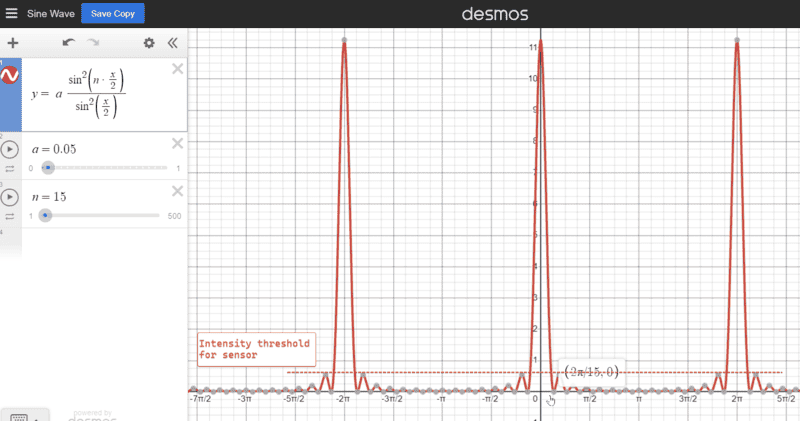
It seems possible to me that if we use a monochromatic red laser with wavelength \lambda=650nm, a reasonably large n = 1500, and a reasonably small "slit-to-imaging-plate distance" r = 20um, by far-field approximation it produces a stripe width w = r \cdot \Delta \phi_{localmin} = 167.55nm < \lambda on the presumed imaging medium.
Is there something I overlooked here that'll prohibit such subwavelength stripe?
There're two possible caveats of the derivation that I'm aware of but not sure whether they're critical enough to break the argument (still checking them theoretically).
I = I_0 \cdot \frac{sin^2(n\phi/2)}{sin^2(\phi/2)}
(quoted from Feynman Lectures Vol I)
Therefore the 2 local minimas adjacent to each global maxima are angularly \Delta \phi_{localmin} = \frac{4\pi}{n} apart. When trying to think of a use case to exploit this formula I got something like this
(the orange dash line marks the threshold intensity below which the imaging medium wouldn't respond)Given an imaging medium whose intensity response is only non-zero when the intensity is above certain threshold, can I cast subwavelength stripes of monochromatic light on it by an n-slit apparatus?
It seems possible to me that if we use a monochromatic red laser with wavelength \lambda=650nm, a reasonably large n = 1500, and a reasonably small "slit-to-imaging-plate distance" r = 20um, by far-field approximation it produces a stripe width w = r \cdot \Delta \phi_{localmin} = 167.55nm < \lambda on the presumed imaging medium.
Is there something I overlooked here that'll prohibit such subwavelength stripe?
There're two possible caveats of the derivation that I'm aware of but not sure whether they're critical enough to break the argument (still checking them theoretically).
- The formula above doesn't take into account the impact from intensity distribution of single slit diffraction, by regarding each single slit just as a perfect point source.
- When having n = 1500, the "slit-to-imaging-plate distance" r = 20um might not be an eligible far-field compared to the total length of all slits, e.g. n \cdot (SlitWidth + SlitPitch) which easily exceeds r for slits of a few microns.