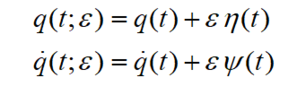Trying2Learn
- 375
- 57
- TL;DR Summary
- Where, in the mathematical work out, do we use the fact that position and velocity are varying independently?
To carry out the machinery of Hamilton's Principle though the calculus of variations, we desire to vary the position and velocity, independently.
We proceed by varying at action, and set the variation to zero (I will assume ONE generalized variable: q1)
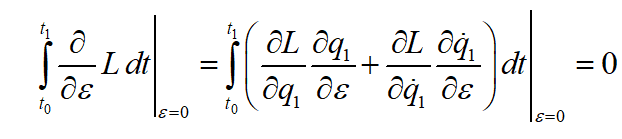
In the above, I can see how we vary both q and q-dot independently: it is (if I am not mistaken) in the "machinery" of taking both partials of q and 1-dot). So far, I am fine with that: it initially appears as if position and velocity were independent.
Then we use integration by parts and obtain
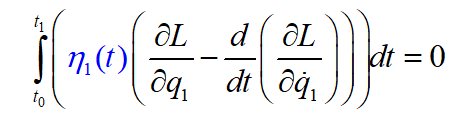
And we extract the Euler Lagrange equation.
However, if I were to look more closely, I see that this work began with:
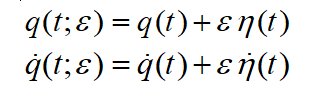
And if this is the case, I do NOT see how q and q-dot are varying independently, because both have the same eta function in their "heritage."
I can see the "intent" that they vary independently (through the "blind"-machinery of taking the partial with respect to q and q-dot, but ultimately, they are not independent, unless the two red functions were different
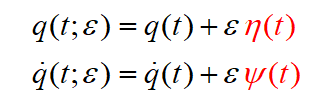
Could someone advise me?
We proceed by varying at action, and set the variation to zero (I will assume ONE generalized variable: q1)
In the above, I can see how we vary both q and q-dot independently: it is (if I am not mistaken) in the "machinery" of taking both partials of q and 1-dot). So far, I am fine with that: it initially appears as if position and velocity were independent.
Then we use integration by parts and obtain
And we extract the Euler Lagrange equation.
However, if I were to look more closely, I see that this work began with:
And if this is the case, I do NOT see how q and q-dot are varying independently, because both have the same eta function in their "heritage."
I can see the "intent" that they vary independently (through the "blind"-machinery of taking the partial with respect to q and q-dot, but ultimately, they are not independent, unless the two red functions were different
Could someone advise me?