Can someone give me some hints for this incline problem?

[DavidFrank]

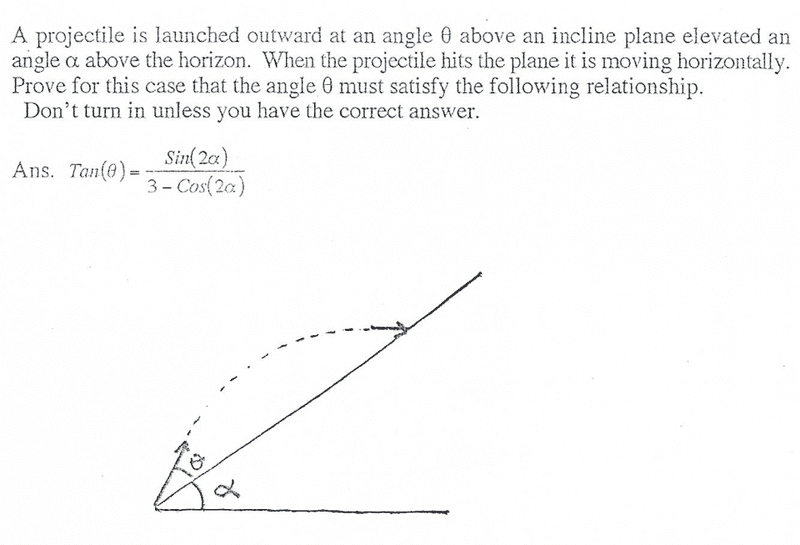
I am sorry, I generally would show some work but I have no clue on how to start off to find angle theta. The answer is given below and I have to get it. I don't know at all how to approach this problem and unfortunately I am not too strong on my trig identities either but I will try. May some please give me some hints?

 

[PeroK]

Forget the complicated answer. Isn't moving horizontally a big clue?

 

[DavidFrank]

Forget the complicated answer. Isn't moving horizontally a big clue?

Oh okay so V_fy = 0 and V_fx = V_fcos(0°) = V_f. Let me think about this some more, thank you.

 

[cnh1995]

You need an equation relating θ and α. Since the ball is at maximum height, horizontal distance traveled is R/2. Do you know the relation between R, H and angle of projection(which is (θ+α) here)?

 

[cnh1995]

Vfx = Vfcos(0°) = Vf.

That is not true. Vx is constant throughout and is equal to Vfcos(θ+α).
You need the relation between θ and α.

 

[haruspex]

That is not true. Vx is constant throughout and is equal to Vfcos(θ+α).
You need the relation between θ and α.

I believe David is using v_f to mean the final velocity.

 

[haruspex]

You need an equation relating θ and α. Since the ball is at maximum height, horizontal distance traveled is R/2. Do you know the relation between R, H and angle of projection(which is (θ+α) here)?

You are introducing new variables without defining them. I assume you are referring to usage in a range equation, in a form standard for you. David might not know this equation, or might not recognise those variable references.
I also guess PeroK is hinting at the same approach.
@DavidFrank , if cnh's post and PeroK's don't help, just apply the usual SUVAT equations for the horizontal and vertical motions. Do you know the SUVAT equations? (You should have listed them in the template.) can you figure out which ones to use?
Please post your working as far as you get.

 

[DavidFrank]

That is so far all I have gotten. My attempt was to find "R" which is the incline distance of this projectile problem. I sort of ran into some issue when I tried finding V_i and substituting it into R = [2sin(θ)cos(θ+ α) * v.i^2] / [g * cos^2(α)] since the R cancels out.

 

[DavidFrank]

You are introducing new variables without defining them. I assume you are referring to usage in a range equation, in a form standard for you. David might not know this equation, or might not recognise those variable references.
I also guess PeroK is hinting at the same approach.
@DavidFrank , if cnh's post and PeroK's don't help, just apply the usual SUVAT equations for the horizontal and vertical motions. Do you know the SUVAT equations? (You should have listed them in the template.) can you figure out which ones to use?
Please post your working as far as you get.

Thank you for your response haruspex, so far I have used the position formula and the V_f^2 = V_i^2 + 2a(Δx) formulas

 

[haruspex]

That is so far all I have gotten. My attempt was to find "R" which is the incline distance of this projectile problem. I sort of ran into some issue when I tried finding V_i and substituting it into R = [2sin(θ)cos(θ+ α) * v.i^2] / [g * cos^2(α)] since the R cancels out.

I can confirm that the answer can be obtained from two of the equations you have developed.
Half way down, you have an equation in which the left hand side consists of sin(α)=. At the end, you have an equation where the left hand side consists of v₀². Work with those.

 

[PeroK]

That is so far all I have gotten. My attempt was to find "R" which is the incline distance of this projectile problem. I sort of ran into some issue when I tried finding V_i and substituting it into R = [2sin(θ)cos(θ+ α) * v.i^2] / [g * cos^2(α)] since the R cancels out.

I must admit I would never have thought of calculating R. The way I looked at it was that the point where it lands is $(x, y)$. I can calculate this from normal projectile motion (it's the top of the trajectory). And I know how this point relates to $\alpha$.

Perhaps this isn't the quickest way, but I ignored the answer and got:

$tan(\theta) = \frac{tan(\alpha)}{1+2tan^2(\alpha)}$

You could shoot for this if you like. Then, use a bit of trig manipulation to get the answer you need.

It looks better than to me than the answer given, not least because it is equivalent to:

$tan(\alpha + \theta) = 2tan(\alpha)$ (Which I find the most pleasing answer!)

 

[DavidFrank]

I can confirm that the answer can be obtained from two of the equations you have developed.
Half way down, you have an equation in which the left hand side consists of sin(α)=. At the end, you have an equation where the left hand side consists of v₀^{2[/SUP?]. Work with those.}

<sup>I am sorry but I am stuck. Do you want to me to take a few steps back before I found "R" (the distance traveled on the incline) or should I keep on going by using V_fy2 = V_iy2 + 2g(Y_f - Y_i)?

Because if I were to continue with the substitution of V_i^2 into "R" I'd get:

1 = [4 * sinΘ * sinα * cos(θ+α)] / [cos2α * sin2(θ+α)]

From here I feel willing to move all of the trig functions with (θ+α) to one side then separate them using the trig identity: cos (θ+α)=( cos θ)( cos α) – ( sin θ)( sinα) & sin (θ+α)=( sin θ)( cos α) + ( sinα)( cosθ) so that I can later group all the trig functions with θ and set it = to all the trig function with α, but it seems like a dead end. So can you please provide more hints on what you are saying before?</sup>

 

[cnh1995]

Here's another way of doing it.
Horizontal displacement is x=R/2 and vertical displacement is H (R is for range and H is for maximum height).
If you take ratio of the expressions of R and H, you'll see
Rtan(Φ)=4H(a standard result!), where Φ is the angle of projection. In your problem, Φ=θ+α.
So,
Rtan(θ+α)=4H
Hence, xtan(θ+α)=2H where x=R/2.
tan(θ+α)=2H/x.
You can write the ratio H/x in terms of angle α(simple trigonometry) and do some trigonometric manipulations to get the final answer.

 

[DavidFrank]

Looking at my teacher's notes, he did this:

cos(θ+α)*cosθ - sinθ*sin(θ+α) = 0

Here's another way of doing it.
Horizontal displacement is x=R/2 and vertical displacement is H (R is for range and H is for maximum height).
If you take ratio of the expressions of R and H, you'll see
Rtan(Φ)=4H(a standard result!), where Φ is the angle of projection. In your problem, Φ=θ+α.
So,
Rtan(θ+α)=4H
Hence, xtan(θ+α)=2H where x=R/2.
tan(θ+α)=2H/x.
You can write the ratio H/x in terms of angle α(simple trigonometry) and do some trigonometric manipulations to get the final answer.

Thank you, I will give this a shot when I return home.

 

[haruspex]

1 = [4 * sinΘ * sinα * cos(θ+α)] / [cos²α * sin²(θ+α)]

That equation is correct and does lead to the answer, though it is a struggle. I must have come a shorter way from the two equations I mentioned in post #10. (And as others have noted, there are easier ways to approach the whole question, but my preference is to help the OP finish their chosen path first.)
From the equation above, I got rid of all the cos and sin by writing t=tan theta, u= tan alpha. You can then get the whole equation in terms of t and u, using cos²=1/(1+tan²).
After some cancellation, you can get the whole thing into the form (...)²=0, affording an immediate simplification.

Looking at my teacher's notes, he did this:
cos(θ+α)*cosθ - sinθ*sin(θ+α) = 0

As a general formula? That would not be right. The left hand side equates to cos(2θ+α). Do you mean your teacher got the equations into this form?