Can someone me understand Norms in number theory?

[Firepanda]

Here is a section of examples from my lecture notes.

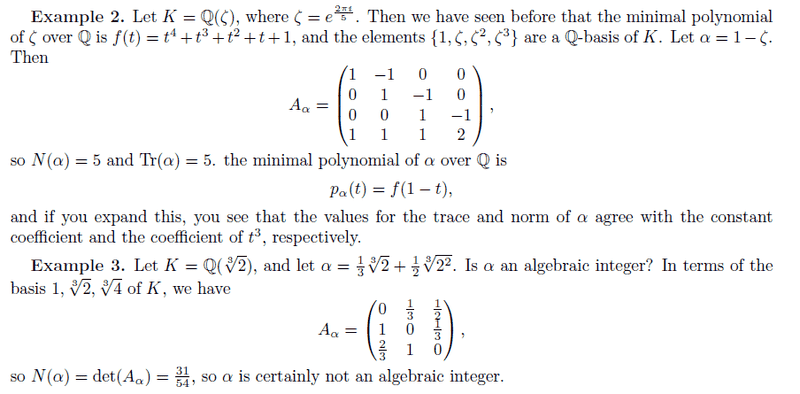
Basically I have NO idea how the lecturer created the matrix A_α, and it's not clear anywhere in the lecture notes.

I think it's something to do with complex embeddings but I'm not sure. Does anyone know?

I'm sure once I know how the matrix was created I can work out the Norms, but so far I'm completely stuck!

 

[jedishrfu]

not sure how to create it either but the first row looks like the coefficients of the alpha = equation namely 0 * 1 + 1/3 * 2^(1/3) + 1/2 4^(1/3) ==> 0, 1/3, 1/2

 

[morphism]

Your lecturer seems to be following an unusual convention. The matrices he's written down really ought to be transposed. What's going on here is that $A_\alpha$ is the multiplication-by-$\alpha$ linear operator on the Q-vector space K. The given matrices are simply the (transposes) of the matrices of $A_\alpha$ with respect to the given bases.

In the first example, we have
$$\begin{align} A_\alpha 1 &= 1 - \zeta \\ A_\alpha \zeta &= \zeta - \zeta^2 \\ A_\alpha \zeta^2 &= \zeta^2 - \zeta^3 \\ A_\alpha \zeta^3 &= \zeta^3 - \zeta^4 = \zeta^3 - (-1 - \zeta - \zeta^2 - \zeta^3) = 1 + \zeta + \zeta^2 + 2\zeta^3\end{align}$$ so the matrix of $A_\alpha$ with respect to the basis $\{1,\zeta,\zeta^2,\zeta^3\}$ is the transpose of the first matrix in your notes. (At least, according to the usual convention of writing down matrices of linear maps wrt given bases. Your lecturer seems to be writing down the entries of the matrix as rows instead of columns. In any case, this doesn't affect the value of the norm or trace, because $N(\alpha) = \det A_\alpha = \det A_\alpha^t$ and similarly $\text{Tr}\,(\alpha) = \text{trace}\, A_\alpha = \text{trace}\, A_\alpha^t$.)

 

[Firepanda]

Awesome thanks! I think I get it now

Say for the first example if I had
$\alpha = \zeta + \zeta^2$

so the matrix of $A_\alpha$ with respect to the basis $\{1,\zeta,\zeta^2,\zeta^3\}$

would be

$A_\alpha$ = [0 1 1 0 ; 0 0 1 1 ; -1 -1 -1 0 ; 1 0 0 0]

Correct? (per the way my lecturer is doing it)

I calculate this as having a norm of 0, is this ok?

 

[morphism]

No - you have a mistake. The give-away is that the norm of a nonzero $\alpha$ can never be zero. (Because $N(\alpha)N(\alpha^{-1})=1$.)

Your first [STRIKE]two[/STRIKE] three rows are right, but your last [STRIKE]two[/STRIKE] one isn't. Note that $\zeta^5=1$.

 

[Firepanda]

No - you have a mistake. The give-away is that the norm of a nonzero $\alpha$ can never be zero. (Because $N(\alpha)N(\alpha^{-1})=1$.)

Your first [STRIKE]two[/STRIKE] three rows are right, but your last [STRIKE]two[/STRIKE] one isn't. Note that $\zeta^5=1$.

Yep sorry, mistake in my calculation, i was focusing on calculating $\zeta^5=1$ and forgot about my $\zeta^4$ term

My last row should be [0 -1 -1 -1]

So my norm should be -1 and trace is -2? Are negatives ok?

A quick way of calculating the rows (or columns in your case) seems to be by shifting them to the right providing there is a 0 to shift into, when there isn't a 0 in the row then a new pattern starts, is that how it is? Seems like that so far!

 

[morphism]

Yep sorry, mistake in my calculation, i was focusing on calculating $\zeta^5=1$ and forgot about my $\zeta^4$ term

My last row should be [0 -1 -1 -1]

So my norm should be -1 and trace is -2? Are negatives ok?

Yup, looks good.

A quick way of calculating the rows (or columns in your case) seems to be by shifting them to the right providing there is a 0 to shift into, when there isn't a 0 in the row then a new pattern starts, is that how it is? Seems like that so far!

Unfortunately that's not how it is in general. The examples here are nice for two reasons: 1) the given bases are "power bases" (i.e. bases of the form {1,x,x^2,...,x^n} for some x), and 2) the given $\alpha$'s are written in terms of the respective bases.