- #1
Topgun_68
- 34
- 0
Homework Statement
I know this is the description of a bipartite graph:
A bipartite graph G is a simple graph whose vertex set can be partitioned into two mutually disjoint nonempty subsets V1 and V2 such that vertices in V1 may be connected to vertices in V2, but no vertices in V1 are connected to other vertices in V1 and no vertices in V2 are connected to other vertices in V2
The Attempt at a Solution
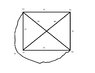
Since a simple graph has no loops or parallel edges, than the attached photo must not be a bipartite graph, correct? Thanks for any feedback!
My scanner is broke so I apologize for the lame drawing :<)