Can the kinetic energy be a function of the position vector?

[jiaodaonline]

Hi guys,
I got one confusion when reading Goldstein's Classical Mechanics (page 20, third edition). After getting the equation,

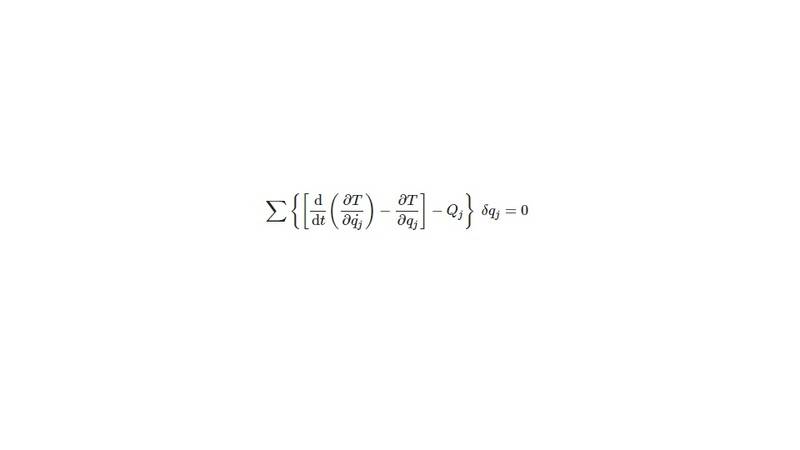
then it says that

Note that in a system of Cartesian coordinates the partial derivative of T with respect to qj vanishes. Thus, speaking in the language of differential geometry, this term arises from the curvature of the coordinates qj. In polar coordinates, e.g., it is in the partial derivative of T with respect to an angle coordinate that the centripetal acceleration term appears.

My question is: Is the above statement general, i.e., that the kinetic energy T does not depend on the position. I wonder why velocity can't depend on the particle's position vector. I mean, why couldn't we have cases where v(x, y, z, t), so that the kinetic energy depends on qj or r?

 

[ShayanJ]

The point is that partial derivatives only care about the explicit dependence of one variable on another. So If you have $y=f(a,b)$ and $a=g(x)$, then $\frac{\partial y}{\partial x}=0$ but $\frac{d y}{d x}= \frac{\partial y}{\partial a} \frac{d a }{d x}$.

 

[jiaodaonline]

only care about the explicit dependence of one variable on another

The point is that partial derivatives only care about the explicit dependence of one variable on another. So If you have $y=f(a,b)$ and $a=g(x)$, then $\frac{\partial y}{\partial x}=0$ but $\frac{d y}{d x}= \frac{\partial y}{\partial a} \frac{d a }{d x}$.

Thanks Shyan!
In my opinion,
if $\vec v=\vec v(x,y,z,t)$, then according to $T=\frac{1}{2} mv^2$,we have

$$\frac{\partial T}{\partial x}=mv\frac{\partial v}{\partial t}$$.

And in this case, $\frac{\partial T}{\partial x}$ is not zero.

I mean the T might depend explicitly on $t$.

 

[ShayanJ]

In Cartesian coordinates we have $T=\frac 1 2 m (\dot x^2+\dot y^2)$. So, in Cartesian coordinates, T depends explicitly only on $\dot q_i$ and noting else!
But in e.g. polar coordinates we have $T=\frac 1 2 m (\dot \rho^2+\rho^2 \dot \varphi^2)$. So, in polar coordinates, T depends explicitly both on $q_i$ and $\dot q_i$, but not on time.

 

[Daz]

Sorry to but-in.

The point is that partial derivatives only care about the explicit dependence of one variable on another. So If you have $y=f(a,b)$ and $a=g(x)$, then $\frac{\partial y}{\partial x}=0$ but $\frac{d y}{d x}= \frac{\partial y}{\partial a} \frac{d a }{d x}$.

I don't think that's correct, at least not in general. If f() depends on a() and a() depends on x then f depends on x. You can use the chain rule, or if you know the form of a() you could simply substitute it into the expression for f(). Either method will give you the correct partial derivative. Simply ignoring the dependence of f() on x because it isn’t “explicit enough” will give you the wrong answer (unless you are treating a and b as independent variables.)

I would say that the correct answer to the OP’s question is this. Recall the definition of partial derivative. The partial derivative of f(a,b,c) with respect to a, for example, is the change in f when we make an infinitesimal change in a while holding the other independent variables constant, divided by the change in a.

Now, in Langrangian mechanics we take the q and q-dot to be our independent variables. That is, when I take the partial derivative of T, for example, with respect to q(i) I change q(i) by a tiny delta, keeping all the other q and q-dot constant. In any coordinate system where the basis vectors are independent (such as cartesian coordinates), holding all the q-dot constant means that I’m holding the velocity of every particle constant. And in a classical Langrangian, we identify those terms which are quadratic in q-dot as T, thus T is a constant.

Put another way: the partial of T wrt q(i) means calculate the change in T when you nudge q(i) slightly while keeping all the other coordinates and velocities constant. In cartesian coordinates T won’t change if you keep all the generalsied velocities constant.

So the answer to the question posed is: yes velocity can depend on position. But if you take position and velocity as your independent coordinates, then taking a partial derivative wrt one of the position coordinates means holding all of the other position coordinates and all of the velocities constant. In cartesian coordinates that leaves T unchanged.

 

[jiaodaonline]

In Cartesian coordinates we have $T=\frac 1 2 m (\dot x^2+\dot y^2)$. So, in Cartesian coordinates, T depends explicitly only on $\dot q_i$ and noting else!
But in e.g. polar coordinates we have $T=\frac 1 2 m (\dot \rho^2+\rho^2 \dot \varphi^2)$. So, in polar coordinates, T depends explicitly both on $q_i$ and $\dot q_i$, but not on time.

Sorry to but-in.
I don't think that's correct, at least not in general. If f() depends on a() and a() depends on x then f depends on x. You can use the chain rule, or if you know the form of a() you could simply substitute it into the expression for f(). Either method will give you the correct partial derivative. Simply ignoring the dependence of f() on x because it isn’t “explicit enough” will give you the wrong answer (unless you are treating a and b as independent variables.)

I would say that the correct answer to the OP’s question is this. Recall the definition of partial derivative. The partial derivative of f(a,b,c) with respect to a, for example, is the change in f when we make an infinitesimal change in a while holding the other independent variables constant, divided by the change in a.

Now, in Langrangian mechanics we take the q and q-dot to be our independent variables. That is, when I take the partial derivative of T, for example, with respect to q(i) I change q(i) by a tiny delta, keeping all the other q and q-dot constant. In any coordinate system where the basis vectors are independent (such as cartesian coordinates), holding all the q-dot constant means that I’m holding the velocity of every particle constant. And in a classical Langrangian, we identify those terms which are quadratic in q-dot as T, thus T is a constant.

Put another way: the partial of T wrt q(i) means calculate the change in T when you nudge q(i) slightly while keeping all the other coordinates and velocities constant. In cartesian coordinates T won’t change if you keep all the generalsied velocities constant.

So the answer to the question posed is: yes velocity can depend on position. But if you take position and velocity as your independent coordinates, then taking a partial derivative wrt one of the position coordinates means holding all of the other position coordinates and all of the velocities constant. In cartesian coordinates that leaves T unchanged.

Thanks a lot to both of you. Actuall, I got another understanding of this

suppose $L=L(q,\dot{q})$, q may depend explicitly on $x$

when we calculate $\frac{\partial L}{\partial x}$, we could first bear in mind that $L=L(q,\dot{q},x)$.
And in order to calculate $\frac{\partial L}{\partial x}$, we should keep $q,\dot{q}$ unchanged. This makes changes in L vanishes. And thus $\frac{\partial L}{\partial x}=0$

PS:I saw Daz post a reply but it is long. So I decided to write my opinion first and then go over Daz's post. I found that what I have posted is exactly what Daz said.

 

[jiaodaonline]

Sorry to but-in.
I don't think that's correct, at least not in general. If f() depends on a() and a() depends on x then f depends on x. You can use the chain rule, or if you know the form of a() you could simply substitute it into the expression for f(). Either method will give you the correct partial derivative. Simply ignoring the dependence of f() on x because it isn’t “explicit enough” will give you the wrong answer (unless you are treating a and b as independent variables.)

I would say that the correct answer to the OP’s question is this. Recall the definition of partial derivative. The partial derivative of f(a,b,c) with respect to a, for example, is the change in f when we make an infinitesimal change in a while holding the other independent variables constant, divided by the change in a.

Now, in Langrangian mechanics we take the q and q-dot to be our independent variables. That is, when I take the partial derivative of T, for example, with respect to q(i) I change q(i) by a tiny delta, keeping all the other q and q-dot constant. In any coordinate system where the basis vectors are independent (such as cartesian coordinates), holding all the q-dot constant means that I’m holding the velocity of every particle constant. And in a classical Langrangian, we identify those terms which are quadratic in q-dot as T, thus T is a constant.

Put another way: the partial of T wrt q(i) means calculate the change in T when you nudge q(i) slightly while keeping all the other coordinates and velocities constant. In cartesian coordinates T won’t change if you keep all the generalsied velocities constant.

So the answer to the question posed is: yes velocity can depend on position. But if you take position and velocity as your independent coordinates, then taking a partial derivative wrt one of the position coordinates means holding all of the other position coordinates and all of the velocities constant. In cartesian coordinates that leaves T unchanged.

Dear Daz,
While I hold the same opinion with Shyan on his example that $\frac{\partial f} {\partial x}$ should be zero. Because according to our discussion, when calculating $\frac{\partial f} {\partial x}$, we should keep $a$ and $b$ unchanged, which makes the change in $f$ vanishes(changes with $a$ and $b$ fixed). But the total derivative with respect to $x$ must be non-zero and calculated by using the chain rule.

 

[Daz]

That depends on what a(x) is and which variables you are taking as independent. Since the functional form of a(x) was not specified, the discussion is general and my point is that the equation given by Shyan does not hold for arbitrary a(x). Consider, for example the trivial case where a(x)=1+2x. You cannot vary x while holding a(x) constant.

 

[jiaodaonline]

That depends on what a(x) is and which variables you are taking as independent. Since the functional form of a(x) was not specified, the discussion is general and my point is that the equation given by Shyan does not hold for arbitrary a(x). Consider, for example the trivial case where a(x)=1+2x. You cannot vary x while holding a(x) constant.

In my opinion, by the definition of $\frac{\partial f} {\partial x}$, we should calculate the changes in $f$ over changes in $x$ under the condition that both $a$ and $b$ are fixed. But as you said, we can't fix $a(x)$ unchanged while changing $x$ in the case of $a(x)=1+2x$. So I think in this case $\frac{\partial f} {\partial x}$ is nonsense in mathematics.