BlackMelon
- 43
- 7
Hi there!
Recently, I have been reading about polarization of a wire's insulator. First of all, I want to see a connection between the last Maxwell's Equation:
$$\nabla\times\\B\ =\mu_0\ J\ +\mu_0\ \epsilon_0\ \frac{\partial E}{\partial t}$$
and the polarization.
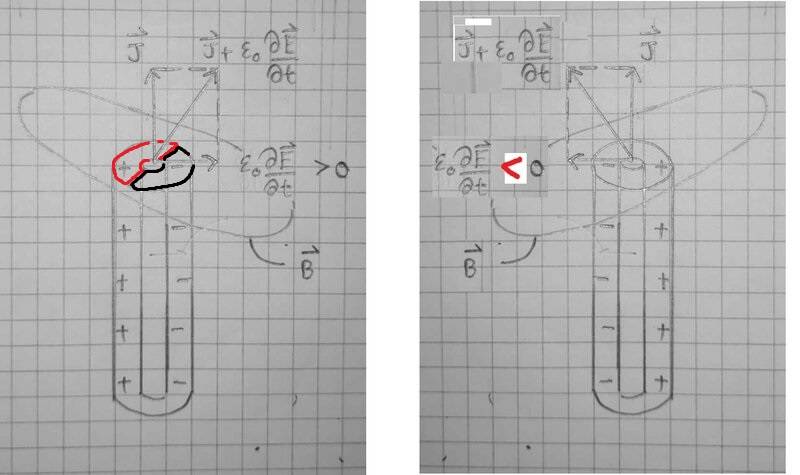
So I draw a simple cartoon below. Here, there is a wire carrying current J.
The inner cylinder is a conductor. The outer shell is an insulator.
Somehow the insulator get polarized (may be by external charges or whatever) such that + is on the red side - is on the black side.
The red and the black keeps swapping themselves back and forth, so does their electric field.
After I summed J and dE/dt and apply the Maxwell's last equation, I found the magnetic field B like a disc, tilting back and forth.
I would like to know if the scenario I made is correct?
If so, could you please suggest any scenario else to explain this equation?
Best
BlackMelon
Recently, I have been reading about polarization of a wire's insulator. First of all, I want to see a connection between the last Maxwell's Equation:
$$\nabla\times\\B\ =\mu_0\ J\ +\mu_0\ \epsilon_0\ \frac{\partial E}{\partial t}$$
and the polarization.
So I draw a simple cartoon below. Here, there is a wire carrying current J.
The inner cylinder is a conductor. The outer shell is an insulator.
Somehow the insulator get polarized (may be by external charges or whatever) such that + is on the red side - is on the black side.
The red and the black keeps swapping themselves back and forth, so does their electric field.
After I summed J and dE/dt and apply the Maxwell's last equation, I found the magnetic field B like a disc, tilting back and forth.
I would like to know if the scenario I made is correct?
If so, could you please suggest any scenario else to explain this equation?
Best
BlackMelon