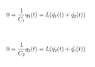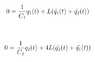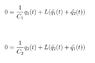Can the Sum of Second Derivatives of Charges be Claimed in a CLC Circuit?

[ForumGuy]

1. The problem statement, all variables and given/known data

Homework Equations

Capacitor (C): v(t) = (1/c)*q(t)
Inductor (L): v(t) = L(d^2q(t)/dt^2)

The Attempt at a Solution

Using Kirchoff's Loop law, the sum of voltages around each loop must be 0. I think I can thus claim the following:

But I'm not so sure I can add the two 2nd derivatives of the charges like that. IF, however, this is true, then can I also claim that q_1(t)/C_1 = q_2(t)/C_2, by subtracting the two equations (or just setting them equal to each other?).

I'm new to Physics Forums, though I've read a lot on here, so let me know if I'm violating any rules! Thanks in advance!

 

[scottdave]

Think about the rules of derivatives. Would you say that $\frac {d} {dt} {(f(t) + g(t))}$ the same as $\frac {d} {dt} {f(t)} + \frac {d} {dt} {g(t)}$ ?
If so then I think you have your answer. How would you apply this to 2nd derivatives?

Also look at the "wire" between the inductor and the capacitor. For an ideal wire, how much voltage drop is there across that?