Casian
- 1
- 0
Hello
I would like to ask here because I couldn't find an answer anywhere on the internet. I recently noticed that two fusion equations have a very good reciprocal cycle, namely the equation: 1H + 2H = 3He, and the equation 3He + 2H = 4He + 1H. I understand that it may have practical limitations, each of the reactions has a different temperature of maximum efficiency and in terms of fuel they would be mostly deuterium which would lead to unwanted mutual fusion of D + D, even so I think it is definitely interesting. Additionally, one such cycle would produce 23.8 MeV which is close to one P + P cycle in the sun. So what is your opinion on it? (I also attach my own graphic for understanding)
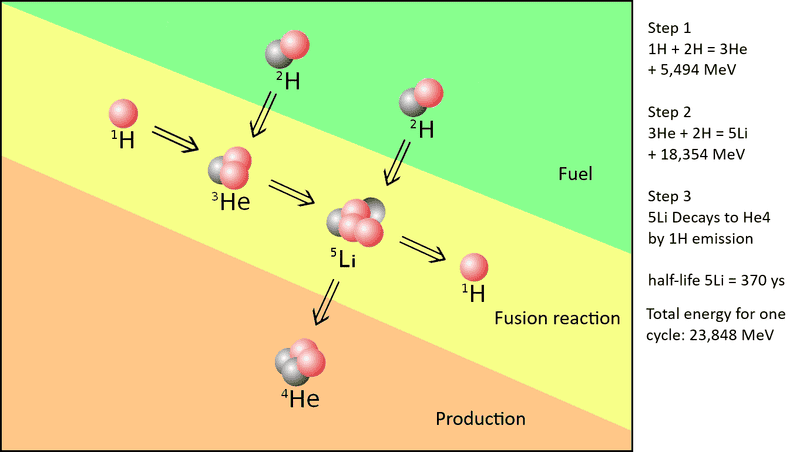
I would like to ask here because I couldn't find an answer anywhere on the internet. I recently noticed that two fusion equations have a very good reciprocal cycle, namely the equation: 1H + 2H = 3He, and the equation 3He + 2H = 4He + 1H. I understand that it may have practical limitations, each of the reactions has a different temperature of maximum efficiency and in terms of fuel they would be mostly deuterium which would lead to unwanted mutual fusion of D + D, even so I think it is definitely interesting. Additionally, one such cycle would produce 23.8 MeV which is close to one P + P cycle in the sun. So what is your opinion on it? (I also attach my own graphic for understanding)