I Can time be another basis vector under Galilean relativity?

[Saw]

TL;DR Summary

Validity of some descriptions shown in the Web where time is a vector in Galilean relativity

I refer to the video of this page, where there is a description of Galilean relativity that is meant to be an introduction to SR, making the comprehension of the latter easier as a smooth evolution from the former.

All the series is in my opinion excellent, but I think that this aspect is flawed.

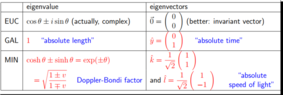
It seems that the idea of the video is assuming that also under Galilean relativity there is spacetime as a vector space, composed of time and space vectors, which would be spanned by bases composed of a time basis vector e_t and another (simplifying the three spatial dimensions into one) e_x.

I will explain what the video does, with some adaptations, to make it simpler.

Imagine that the platform is a blue basis and the train is a red basis. The train is displacing wrt to the platform at v = ½ m/s. Event 1 is when the mid-points of the platform and train are instantaneously aligned, and we fix at that point the origins of the two reference frames. Event 2 happens at (common) time t = 2 s, but at x = 1 in the train frame.

To infer the Galilean transformation from red into blue, one can, for example, proceed as follows:

- Measure the (origin) red basis vectors in terms of the (destination) blue basis vectors (assumed to be unitary), as follows:

\color{red}{e_x} = (\color{blue}{e_x},0) = (1,0)
\color{red}{e_t} = (\color{blue}v{e_x},{e_t}) = (v,1)

- Put these values as column vectors of the change of basis matrix:
\left( {\begin{array}{*{20}{c}}<br /> \color{blue}{x}\\<br /> \color{blue}{t}<br /> \end{array}} \right) = \left( {\begin{array}{*{20}{c}}<br /> 1&amp;v\\<br /> 0&amp;1<br /> \end{array}} \right)\left( {\begin{array}{*{20}{c}}<br /> \color{red}{x}\\<br /> \color{red}{t}<br /> \end{array}} \right) = \left( {\begin{array}{*{20}{c}}<br /> {1*\color{red}{x} + v*\color{red}{t}}\\<br /> {0*\color{red}{x} + 1*\color{red}{t}}<br /> \end{array}} \right) = \left( {\begin{array}{*{20}{c}}<br /> {\color{red}{x} + v\color{red}{t}}\\<br /> \color{red}{t}<br /> \end{array}} \right) = \left( {\begin{array}{*{20}{c}}<br /> {\color{red}{1} + 0.5*\color{red}{2}}\\<br /> \color{red}{2}<br /> \end{array}} \right) = \left( {\begin{array}{*{20}{c}}<br /> \color{blue}{2}\\<br /> \color{blue}{2}<br /> \end{array}} \right)

The video also talks about an invariant spacetime interval which would be the arrow joining events 1 and 2, built as the addition of the time and space intervals in each frame, with this mathematical expression:

\vec S = \color{red}{x{\vec e_x}} + \color{red}{t{\vec e_t}} = \color{blue}{x{\vec e_x}} + \color{blue}{t{\vec e_t}}

However, despite the beauty of the attempt, my opinion is that it obscures instead of clarifying the transit from Galilean to SR. The shift of paradigm represented by SR is precisely that in the Galilean context the vectors existed only for the spatial dimensions, time being a different thing, not a homogeneous unit that you could combine with space units.

Some thoughts to support this claim:

- The above-mentioned Galilean spacetime interval is useless, since it does not solve any practical problem.

- One can say that the “metrics” of space and time in Galilean relativity are different. But why? In SR we homogenize time and space units by multiplying time by the invariant speed of light c. There is no invariant speed in the Galilean framework. Anyhow, the author of the video claims in some comments that he can multiply space units by any arbitrary speed, preferably unitary to keep the numerical value of the time units, like c = 1 m/s. I am convinced that this is unacceptable but it would be interesting to specify why.

Which position would you take and how would you support it?

EDIT: I have later realized that in the next session of the series the author does admit that there is no sensible Galilean spacetime "distance". In fact, he talks about a ST "separation" vector. The question is still why to talk about a ST "whatever" vector containing components that are not recomposed to find any problem-solving magnitude.

 

[anuttarasammyak]

I understand that Galilean transformation conserves time and space independently
\triangle t = \triangle t&#039; and \triangle l = \triangle l&#039;
for simultaneous events which are compared with SR's
\triangle s = \triangle s&#039;

 

[PeroK]

I don't see anything particularly wrong with the approach. The main issue is that if the student needs the amount of mathematical hand-holding that the presenter assumes, then they are in no position to study GR anytime soon.

That you are critically analysing the video suggests that you might be better off with more focused material. How did you chose these lectures?

 

[Saw]

I understand that Galilean transformation conserves time and space independently
\triangle t = \triangle t&#039;, \triangle l = \triangle l&#039;
comparing with SR's
\triangle s = \triangle s&#039;

So would you disagree with the video? Given that the latter claims that there is a Galilean
\triangle s = \triangle s&#039;

 

[Saw]

I don't see anything particularly wrong with the approach.

So you would agree with the video? And hence agree that in Galilean relativity space and time have the same metric and that you can combine them into a meaningful spacetime interval?

 

[anuttarasammyak]

Sorry, I will watch it soon but for now I think
since c is regarded infinite limit in Galilean transformation, SR invarant relation
\triangle s =\triangle s&#039;
tell about comparizon of time conponents which have coefficient c.
\triangle t =\triangle t&#039;
In case $\triangle t =\triangle t'=0$ which can happen by absolute simuntaneity in Galilean trasformation, spatial part matters so
\triangle l =\triangle l&#039;
Anyway I will watch it.

 

[PeroK]

So you would agree with the video? And hence agree that in Galilean relativity space and time have the same metric and that you can combine them into a meaningful spacetime interval?

Did he claim that?

 

[Ibix]

I believe that it is possible to frame Galilean relativity in terms of geometry and get Newtonian gravity in terms of spacetime curvature. It's called Newton-Cartan gravity, and there's an Insight about it here. So it's a concept with legs, even if not one of the most widely studied.

As @PeroK says, I don't think there's anything mathematically wrong with the concept. And there's nothing wrong with drawing comparisons between relativity and a slightly unusual way of looking at pre-relativistic physics. I agree it's not as powerful a formalism as the metric view of relativity is, but it's probably not without value. If you don't find it useful, though, shrug and move on.

 

[PeroK]

Did he claim that?

It's clear that in two frames we can have:
$$\Delta t = \Delta t', \ \Delta x = 0, \ \Delta x' = vt$$And, in general, there is no invariant quantity (other than $\Delta t$ itself).

 

[vanhees71]

This is just a convenient way to write the Galilei transformations, including boosts, as matrix operations on column vectors. Nevertheless there's no more structure to these 4D vectors in Newtonian physics, i.e., there's only the positive definite scalar product for the spatial 3D vectors.

Galilei-Newton spacetime is not an affine space or a (pseudo-)Riemannian space as in SRT and GRT, respectively, but a fiber bundle, i.e., at each time there's a 3D Euclidean affine space to describe the space. Time itself is an oriented 1D affine space, independent of the 3D affine space that describes space. In this sense time is absolute as well as space in Newtonian physics.

 

[robphy]

This is just a convenient way to write the Galilei transformations, including boosts, as matrix operations on column vectors. Nevertheless there's no more structure to these 4D vectors in Newtonian physics, i.e., there's only the positive definite scalar product for the spatial 3D vectors.

Galilei-Newton spacetime is not an affine space or a (pseudo-)Riemannian space as in SRT and GRT, respectively, but a fiber bundle, i.e., at each time there's a 3D Euclidean affine space to describe the space. Time itself is an oriented 1D affine space, independent of the 3D affine space that describes space. In this sense time is absolute as well as space in Newtonian physics.

https://www.physicsforums.com/threads/what-exactly-are-invariants.1045392/post-6799064

Again? ...
In short: it's both a fiber bundle and an affine space.

---

[Reference to eigenchris's YouTube video
Relativity 103c: Galilean Relativity - Galilean Transform and Covariance/Contravariance ]

However, despite the beauty of the attempt, my opinion is that it obscures instead of clarifying the transit from Galilean to SR. The shift of paradigm represented by SR is precisely that in the Galilean context the vectors existed only for the spatial dimensions, time being a different thing, not a homogeneous unit that you could combine with space units.

Some thoughts to support this claim:

- The above-mentioned Galilean spacetime interval is useless, since it does not solve any practical problem.

- One can say that the “metrics” of space and time in Galilean relativity are different. But why? In SR we homogenize time and space units by multiplying time by the invariant speed of light c. There is no invariant speed in the Galilean framework. Anyhow, the author of the video claims in some comments that he can multiply space units by any arbitrary speed, preferably unitary to keep the numerical value of the time units, like c = 1 m/s. I am convinced that this is unacceptable but it would be interesting to specify why.

Which position would you take and how would you support it?

• Here's my very old poster on "Spacetime Trigonometry" (which I really should write up and publish)
  https://www.aapt.org/doorway/Posters/SalgadoPoster/Salgado-GRposter.pdf
  where the Galilean spacetime has a geometry intermediate between Euclidean space and Minkowski spacetime (in the Cayley-Klein classification of geometries ).
  
  The above is part of the ancient set of partially-working webpages for the
  "AAPT Topical Workshop: Teaching General Relativity to Undergraduates" (2006) https://www.aapt.org/doorway/Posters/posters.htm and https://www.aapt.org/doorway/TGRU/ ).
• Attached to the above poster (p. 1-19) is a 2006 draft (on p. 20-27 )
  "Spacetime Trigonometry and Analytic Geometry I: The Trilogy of the Surveyors"
  https://www.aapt.org/doorway/Posters/SalgadoPoster/Salgado-GRposter.pdf#page=20
  which distinguishes c_{light} (a conversion constant) and c_{light} (maximum signal speed) and addresses your question.
  (see this ancient post from 2007:
  https://www.physicsforums.com/threads/spacetime-interval-of-zero.180504/post-1402877 )
• This idea is visualized in my "spacetime diagrammer"
  https://www.desmos.com/calculator/kv8szi3ic8
  where you can vary the E-parameter from Euclidean (E=-1) and Minkowski (E=+1) where Galilean is (E=0).
  In the above desmos visualization, the metric is encoded in the "unit circle"
  $$y^{2}-Ex^{2}=1.$$
• I have been actively working out aspects of this "spacetime trigonometry" idea to use the Galilean spacetime as a bridge to the Minkowski spacetime, and then, maybe someday, to the de Sitter spacetimes.
  The target audiences would be undergraduates and beginning graduate students.
  
  The idea is that one can try to formulate and solve a typical physics problem
  in a "unified trigonometric" way using the same [spacetime-informed] intuition,
  which will give the PHY 101 answer in Galilean geometry
  and the PHY 201 answer in Special Relativity,
  using ideas and techniques borrowed from MATH 101 (Euclidean Geometry).
  
  (The above poster gives examples. I am seeking to apply this to more physics problems.)
• In short, I think the approach is consistent.

 

[Saw]

Answering all through vanhees71' comment, since it is the most complete and the rest seem to agree with it:

This is just a convenient way to write the Galilei transformations, including boosts, as matrix operations on column vectors.

I have no problem with the use of a matrix to write the Galilean transformation. You can also use a matrix to describe a translation (thanks to the "homogeneous coordinates" method, where you add a new dimension with value 1), but nobody would say that a distance is a linear combination of X with that sort of ghost dimension. Similarly here with the purported Galilean time dimension.

Time itself is an oriented 1D affine space, independent of the 3D affine space that describes space.

I would conclude then that you don't agree with the approach of the video, which means precisely placing time and space in the same 4D affine space, containing its own invariant interval.

 

[vanhees71]

That indeed doesn't make sense in Newtonian spacetime.

 

[Saw]

https://www.physicsforums.com/threads/what-exactly-are-invariants.1045392/post-6799064

Again? ...
In short: it's both a fiber bundle and an affine space.

I see that there has been a very technical debate among mentors about this...

I would also be very interested in understanding its technicalities if you can bear with me starting from a much lower level. But also, it is my impression that precisely at such a high level of yours, the differences are terminological, i.e. you talk about the same things, but there is no agreement on the terms. In this sort of situations, it usually helps to look at things from a very basic and operational level.

If as OP I have some power to direct the discussion of the thread, I would kindly request you to also pay some attention to this other operational or pragmatic approach, by opining on the two issues that I initially raised:

- Is a Galilean spacetime interval of any use at all? Or rather, isn't it true that the only practical problems that reality can pose are solved, assuming a Galilean universe, by looking at either time or space independently, but never as a combination of the two values?
- In Galilean relativity, can you measure time against space, like for example you can measure space with a clock in SR, or like you can measure kms against miles?

 

[robphy]

Note that a PHY 101 position-vs-time diagram is an affine space
(in the language in my earlier post)
in that one can use vector displacements (in time and in space)
to get from one point-event to another point-event.

Further, this diagram has a non-euclidean geometry

For convenience, let us measure time in seconds and space in units of light-seconds.
(It doesn't matter that the "the speed of light" (as a "maximum signal speed") isn't an invariant in Galilean physics. I am using it as a "conversion-constant".
I could use "sound-seconds", where "1 sound-sec" is 343 meters.
But since my eventual goal is special relativity, I'll choose "light-seconds", where "1 light-sec" is 299792458 meters.)

There are 4 displacement vectors to consider
\vec v_{B}=3\hat t +0 \hat y
\vec v_{G}=3\hat t +1.5 \hat y
\vec v_{R}=3\hat t +3 \hat y
\vec v_{S}=0\hat t +1 \hat y

There is a Galilean spacetime geometry underlying the PHY 101 position-vs-time diagram.

• Let me define a Galilean dot-product as follows
  \vec A \stackrel{G}{\cdot} \vec B = A_tB_t which implies a temporal-magnitude |\vec A|_G=\sqrt{\vec A \stackrel{G}{\cdot} \vec A}.
• This dot-product, however, will assign zero to all vectors with zero time-displacement.
  We need another dot-product to assign nonzero magnitudes to these vectors.
  So, we define a second dot-product as follows
  \vec A \stackrel{S}{\cdot} \vec B = A_yB_y
  which implies a spatial-magnitude |\vec A|_S=\sqrt{\vec A \stackrel{S}{\cdot} \vec A}.
• Note that we could do the same construction with a PV-diagram from thermodynamics.
  (I am not pursuing any attempt to develop for the PV-diagram
  what I am about to do for the PHY101 position-vs-time diagram.)
• Yes, these dot-products are "degenerate" (nonzero vectors may be assigned zero magnitudes),
  which complicates some constructions. However, we proceed carefully.
• Unlike in Euclidean space or Minkowski spacetime,
  these dot-products do not "mix" the time and space coordinates.
  Nevertheless, we can try to carefully proceed with the same strategies.
  (If I want to be completely general about things, I would write
  \vec A \stackrel{G}{\cdot} \vec B \equiv A_tB_t - (0)A_yB_y =A_tB_t,
  as a special case of \vec A \stackrel{CK}{\cdot} \vec B \equiv A_tB_t - (E)A_yB_y.)

---

• Note that \vec v_{B}, \vec v_{G}, \vec v_{R} have the same magnitude of 3[-sec] , in spite of their visual appearances (to a Euclidean eye). However, if we interpret this magnitude as the elapsed time on their wristwatches, then this says that all of these travelers will read a 3-sec elapsed-time on their wristwatches for the motions shown. These vectors are Galilean-congruent... a Galilean boost will map one of these vectors to another.
• Note that \vec v_{B}, \vec v_{G}, \vec v_{R} are all G-perpendicular to \vec v_{S} since \vec v_{S} \stackrel{G}{\cdot}\vec v_{B}=0, etc.,
  in spite of their visual appearances (to a Euclidean eye).
  That is, the dotted-line represents "all space at an instant of time" for each traveler.
• Note that the dotted-curve is actually a "Galilean circle" of radius 3.
  And that the tangent-lines to the circle at the event of each "radius-vector" tip conicide.
  This coincidence of tangent lines is precisely the notion of absolute-simultaneity in Galilean physics.

---

If one didn't care about special relativity, then the above is likely not of much use.
However, if one is trying to make sense of special relativity,
it might be useful to know that one could understand special relativity,
not by throwing everything away ("forgetting all that you know") and starting from zero,
but by re-interpreting (in a "unified" way) Galilean physics geometrically with careful analogies to Euclidean geometry,
as a possibly-useful toy-model of spacetime physics,
as a bridge to special relativity and further.

In this approach, a possibly surprising result in special relativity
can be re-interpreted from its Galilean analgoue (often akin to a Galilean limit),
and, hopefully, suggest that the special relativity result isn't as weird as you might have first thought.

An example from my poster:​

• velocity addition (from the [hyperbolic-]tangent function of a sum):
  v_{AC}=\frac{ v_{AB}+v_{BC}}{ 1 +E\ v_{AB}v_{BC}}
  

 

[Saw]

• I have been actively working out aspects of this "spacetime trigonometry" idea to use the Galilean spacetime as a bridge to the Minkowski spacetime, and then, maybe someday, to the de Sitter spacetimes.
  The target audiences would be undergraduates and beginning graduate students.
  
  The idea is that one can try to formulate and solve a typical physics problem
  in a "unified trigonometric" way using the same [spacetime-informed] intuition,
  which will give the PHY 101 answer in Galilean geometry
  and the PHY 201 answer in Special Relativity,
  using ideas and techniques borrowed from MATH 101 (Euclidean Geometry).
  
  (The above poster gives examples. I am seeking to apply this to more physics problems.)

I am most sympathetic to your idea of building bridges between (passive) transformations and finding a connecting thread between them. I am also embarked since long ago on the project of building an analogy among, not just the Euclidean circle-like rotation, the Galilean boost and the Minkowskian hyperbolic rotation, but also starting from a translation, going through scaling and ending up with Fourier transform...

But I really believe that, even if your diagram finds the Galilean thing in the middle of the story, heuristically the Galilean change of perspective is closer to a translation (if you focus on the relationship between X and T or the whole lot X-Y-Z and T; see my comment above on homogeneous coordinates; you can put X and T together in a matrix, just like you can put X and 1 together in a translation matrix, but that does not mean that they form a basis, since they are not homogeneous; what is more, you don´t solve any problem by combining them) and the Minkowskian one is closer to the Euclidean one (if you accept T as a member of the lot, so that X and T, having now the same metric, can combine together to produce a problem-solving interval).

EDIT: I was drafting my post while you posted yours. This one does not intend to reply to your latest one, which I will have to assimilate.

 

[robphy]

You may have missed by update that gives an example.

velocity addition (from the [hyperbolic-]tangent function of a sum):​

v_{AC}=\frac{ v_{AB}+v_{BC}}{ 1 +E\ v_{AB}v_{BC}}​

​

There is a unified construction and derivation from the identity for the hyperbolic-tangent of a sum that leads to the above unified expression.
With E=-1, you have an equation for slopes in euclidean geometry.
With E=0, you have an equation for velocity addition in Galilean physics.
With E=1, you have an equation for velocity addition in Special Relativity.

This is the type of unified viewpoint that I am working on.

UPDATE:
Here's a rotation (for E=-1) and a boost (for E=0 or E=1) in rectangular coordinates
<br /> R=\left(<br /> \begin{array}{cc}<br /> \frac{1}{\sqrt{1-Ev^2}} &amp; \frac{E\ v}{\sqrt{1-Ev^2}}\\<br /> \frac{v}{\sqrt{1-Ev^2}} &amp; \frac{1}{\sqrt{1-Ev^2}}<br /> \end{array}<br /> \right)<br />
to preserve the unit circle
t^2 - E y^2=1
as in my "spacetime diagrammer" https://www.desmos.com/calculator/kv8szi3ic8 .

 

[vanhees71]

Of course, you can interpret Galilean space-time also as a 4D affine space, but it has no specific additional structure concerning a connection of time and 3D space. Only the 3D space is additionally also an Euclidean affine space. The fiber-bundle interpretation thus is (in some literal sense) "more natural" for its physical interpretation. In Newtonian physics space and time are absolute, while in SRT you have "a kind of union", as was famously said by Minkowski in his famous talk about his reinterpretation of SRT spacetime as an affine pseudo-Euclidean space with Lorentzian signature (1,3) or (3,1), which today is thus called "Minkowski space".

 

[robphy]

Of course, you can interpret Galilean space-time also as a 4D affine space, but it has no specific additional structure concerning a connection of time and 3D space. Only the 3D space is additionally also an Euclidean affine space. The fiber-bundle interpretation thus is (in some literal sense) "more natural" for its physical interpretation. In Newtonian physics space and time are absolute, while in SRT you have "a kind of union", as was famously said by Minkowski in his famous talk about his reinterpretation of SRT spacetime as an affine pseudo-Euclidean space with Lorentzian signature (1,3) or (3,1), which today is thus called "Minkowski space".

With the regard to my Cayley-Klein geometry approach,
regarding Galilean spacetime as an affine geometry (as an intermediate between Euclidean and Minkowski)
allows me to more easily find a unified physics-geometrical relationship and interpretation.
When I am at the E=0-case of the Cayley-Klein geometries, then I recognize a fiber-bundle structure.

(With 20-20 hindsight, I can use the geometry of the E=-1 Euclidean case with the physics of the newly recognized E=0 Galilean case to get to the E=+1 Minkowski case of special relativity.)

(My approach with E provides a one-parameter family of geometrical structures…. which can formalize a notion of a non-relativistic limit—not just in terms of formulas but also in terms of geometry.)

However, from the fiber-bundle viewpoint in the Galilean case,
it may not be so easy to make this physics-geometry connection
since neither Euclidean or Minkowski has a fiber-bundle structure.
We need guidance from elsewhere to relax the fiber-bundle structure to get to special relativity.

 

[Saw]

regarding Galilean spacetime as an affine geometry (as an intermediate between Euclidean and Minkowski)
allows me to more easily find a unified physics-geometrical relationship and interpretation.
When I am at the E=0-case of the Cayley-Klein geometries, then I recognize a fiber-bundle structure.

(With 20-20 hindsight, I can use the geometry of the E=-1 Euclidean case with the physics of the newly recognized E=0 Galilean case to get to the E=+1 Minkowski case of special relativity.)

(My approach with E provides a one-parameter family of geometrical structures…. which can formalize a notion of a non-relativistic limit—not just in terms of formulas but also in terms of geometry.)

First, let me insist that I find your attempt at unification most interesting and the E parameter approach very appealing. I will keep studying it, maybe we can fully treat it in another thread, but also please let me try to concentrate on the object of this one, which is only whether Galilean geometry combines space and time units to get a meaningful spacetime interval.

On the technical side, since I don't know what a "fiber-bundle" structure is, I cannot have an opinion on how it makes unification harder. Maybe you or vanhees71 can provide some elaboration on this.

But I would also kindly ask you to take for a minute the operational / problem-solving approach, which is after all what all concepts, including mathematical ones, are invented for.

In this line, I said that a spacetime interval defined (like in the reference video) as follows...

\vec S = \color{red}{x{\vec e_x}} + \color{red}{t{\vec e_t}} = \color{blue}{x{\vec e_x}} + \color{blue}{t{\vec e_t}}

is good for nothing, since it does not solve any practical problem.

I also said that I do not see an operative conversion factor between Galilean time and space units.

Let me try now to be more specific, thinking aloud:

- If I want to know whether Event 1 can have any influence on Event 1 (or whether a signal transmitted from 1 can reach 2), in the Galilean universe I just look at time. I sometimes hesitate whether (assuming the possibility of an infinite velocity) only a past Event 2 would be out of reach or also a simultaneous Event 2, but in any case the judgment is based only on the (absolute) time measurement of all observers.

- Assuming that Event 1 can influence Event 2, if I need to calculate at what speed (u) I could send a projectile from 1 to 2, that is a little more tricky. I have to take into account the (absolute) time-lapse available btw 1 and 2 (say 2s), as well as the (relative) distance between them (say x = 2m as measured from the train and x' = 3m from the platform, since v = 0.5 m/s). As a minimum, I would need u to be 1 m/s from the train and u' = 1.5 m/s (u + v) from the platform. In a way, I could say that after applying a (relative or variant) speed as "conversion factor" (u and u'), I have concluded that from the perspective of both frames subtracting distance (x o x') from spatialized time (ut or u't) gives zero (x - ut = x' - u't = 0), meaning there can be causal influence with projectiles at the relevant "conversion" speeds. But I did not add up space and time units (in a way, I subtracted) and did not employ any invariant conversion factor, which is impossible to attain, because anything will have a variant speed in Galilean relativity.

In fact, looking at your papers I see that your spacetime interval...

... only includes in the Galilean case the time interval. In other words, the application of your E parameter is confirming that, strictly speaking, there is no Galilean spacetime interval. Indeed this does not diminish the merit of your generalization: it just means that it works in the Galilean domain in a manner that does not entail the addition of space and time. That is why I said (and one just has to look at the image to realize it) that a Minkowskian hyperbolic rotation is closer to a Euclidean circular rotation than to a Galilean boost and that the latter is closer to a translation.

I must still look at what you say about the possibility in the Galilean context of a speed acting as a conversion factor. Maybe you could briefly summarize it.

 

[robphy]

In this line, I said that a spacetime interval defined (like in the reference video) as follows...

\vec S = \color{red}{x{\vec e_x}} + \color{red}{t{\vec e_t}} = \color{blue}{x{\vec e_x}} + \color{blue}{t{\vec e_t}}

is good for nothing, since it does not solve any practical problem.

For clarity of terms and notation, you are describing a displacement-vector in the spacetime-diagram.
The interval or squared-interval is an assignment of a size or [possibly-signed] number to a vector using a dot-product (or associated metric) which is to be preserved by associated rotations or boosts.

Vectors like your \vec S can be used to describe the tangent-vectors to worldlines in the diagram.
With the help of the dot-product, we can normalize the tangent vectors to obtain the Galilean analogue of the so-called 4-velocity for that worldline.
One can think of the size of this 4-velocity as one tick on the worldline's clock, and the direction is obviously important to describe the motion of various objects.
So, even though all Galilean 4-velocities have the same magnitude (same interval) given by the dot-product \stackrel{G}{\cdot} (as defined earlier in #15), such unit-displacement vectors \hat S are useful for practical problems (but one has to know how to use them to appreciate them).

Admittedly, many geometrical constructions may look trivial in the Galilean case.
But this is a warm up to Special Relativity, using the same geometrical constructions with a more complicated dot-product. Again, if one didn't care about Special Relativity, then this is likely of little value.

---

A useful calculation is to find the eigenvectors

• of the rotation matrix. (There are none.)
• of the Lorentz boost (in 1+1 Minkowski).
  There are two, and they correspond to the maximum speed of signal propagation (which happens to also be the speed of light) in the forward and backward directions. The eigenvalues are the Doppler factors.
  (This is the invariance of the speed of light).
  There are no timelike eigenvectors. (This is the principle of relativity.)
• of the Galilean boost (in 1+1 Galilean).
  There is one, and it corresponds to the infinite maximum speed of signal propagation in Galilean physics. The eigenvalue is 1, and it can be associated with absolute-length in Galilean physics.
  There are no timelike eigenvectors. (This is the principle of relativity.)

So, again, in spite of Galilean-vectors not "mixing" space and time in the dot-product or spacetime-interval,
Galilean displacement vectors, which do have time and space components, (e.g. Galilean 4-velocities) are useful for practical problems.

---

As @Ibix mentions in #8 , one can develop Newtonian gravity using the Newton-Cartan approach.
(See my references to Ehlers in https://www.physicsforums.com/threads/geometrized-newtonian-gravity.703510/post-4459094 ; and Trautman in https://www.physicsforums.com/threads/geometrized-newtonian-gravity.703510/post-4459148 .) Gravitation is useful for practical problems.

---

My first interest in Galilean spacetime came from
Jammer and Stachel's "If Maxwell had worked between Ampère and Faraday: An historical fable with a pedagogical moral" American Journal of Physics 48, 5 (1980); https://doi.org/10.1119/1.12239
which is based on work by Levy-Leblond (https://en.wikipedia.org/wiki/Galilean_electromagnetism - not to be confused with a journal with a similar name as I described here ).

---

I also said that I do not see an operative conversion factor between Galilean time and space units.

Earlier (in #15) , I gave an example with "sound-seconds" (343 meters).
Do you have a problem expressing distances in space using that unit?
A lightning strike in the distance could be described in meters or furlongs or sound-seconds.
Sound-seconds are convenient if use my wristwatch (as opposed to a long tape measure) as my main measuring instrument.
Isn't this how sonar works?

There's no use of invariance or relativity-principle being invoked here.
(Indeed, the speed of sound is not invariant under boosts.)
I just want to use convenient units so that I can draw a diagram and
assign magnitudes to \vec S vectors.
I'm not hiding a distinction between space and time.... I'm demoting the standard SI unit for it.

---

I don't have time right now to consider your thinking-out-loud examples.
I may have more time later.

 

[haushofer]

So you would agree with the video? And hence agree that in Galilean relativity space and time have the same metric and that you can combine them into a meaningful spacetime interval?

See e.g. page 36 of the thesis

https://www.google.com/url?sa=t&rct...e_thesis.pdf&usg=AOvVaw3xeIMItlns2gjYN4ANv5Bd

Under the group of Galilean transformations you can only have a separate spatial line element and a temporal line element. There is no spacetime metric, as the calculation on that page shows; you have a so-called "degenerate metric structure", which mathematicians wouldn't even call a metric, I guess.

 

[PeterDonis]

I believe that it is possible to frame Galilean relativity in terms of geometry and get Newtonian gravity in terms of spacetime curvature.

Yes, but that curvature is not derived from a spacetime metric, since there is no spacetime metric in Galilean spacetime. The curvature is derived from a connection, but that connection has nothing to do with any spacetime metric (since there isn't one).

 

[Dale]

Is a Galilean spacetime interval of any use at all?

In Newton Cartan theory spacetime is a 4D manifold equipped with a pair of degenerate metrics, one for time and one for space. Personally, I think that is probably a more fruitful avenue to pursue.

Edit: I see @Ibix already mentioned it!

 

[Saw]

For clarity of terms and notation, you are describing a displacement-vector in the spacetime-diagram.
The interval or squared-interval is an assignment of a size or [possibly-signed] number to a vector using a dot-product (or associated metric) which is to be preserved by associated rotations or boosts.

Vectors like your \vec S can be used to describe the tangent-vectors to worldlines in the diagram.
With the help of the dot-product, we can normalize the tangent vectors to obtain the Galilean analogue of the so-called 4-velocity for that worldline.
One can think of the size of this 4-velocity as one tick on the worldline's clock, and the direction is obviously important to describe the motion of various objects.
So, even though all Galilean 4-velocities have the same magnitude (same interval) given by the dot-product \stackrel{G}{\cdot} (as defined earlier in #15), such unit-displacement vectors \hat S are useful for practical problems (but one has to know how to use them to appreciate them).

Sorry, I did not follow you here.

The spacetime interval that I mentioned (yes, a spacetime displacement vector) is what the author of the video claims to be the invariant interval of Galilean spacetime.

In SR context, I know about the spacetime velocity vector, which is formed by the components of the spacetime displacement vector divided by proper time, right? Apparently, you also find an analog in Galilean context for this vector (even if here there is no distinction btw coordinate and proper time...).

My questions are then:
- the image that I copied from your paper, it is referring to the (squared) spacetime displacement vectors, not to velocity vectors, right?
- if so, it would be true that this displacement vector would not mix time with space, it would only be composed of time?
- then you talk about velocity vectors, which would mix time with space components, because these ones would instead have practical use?

A useful calculation is to find the eigenvectors

• of the rotation matrix. (There are none.)
• ....
• of the Galilean boost (in 1+1 Galilean).
  There is one, and it corresponds to the infinite maximum speed of signal propagation in Galilean physics. The eigenvalue is 1, and it can be associated with absolute-length in Galilean physics.
  There are no timelike eigenvectors. (This is the principle of relativity.)

So, again, in spite of Galilean-vectors not "mixing" space and time in the dot-product or spacetime-interval,
Galilean displacement vectors, which do have time and space components, (e.g. Galilean 4-velocities) are useful for practical problems.

Above you say that the eigenvector of the Galilean boost is the infinte speed. I preferred what I read in your draft paper (see below) which is that the eigenvector is absolute time. I was going to comment that for me that was something that had always been in the back of my mind. Is there a mistake somewhere or did you change your mind?

So, again, in spite of Galilean-vectors not "mixing" space and time in the dot-product or spacetime-interval,
Galilean displacement vectors, which do have time and space components, (e.g. Galilean 4-velocities) are useful for practical problems.

I did not follow this, either. Here you seem to make a distinction btw Galilean vectors (not mixing space and time, perfect for me) and Galilean velocities (mixing space and time, purportedly having utility, to be clarified), so far so good, but you refer to the latter as displacement vectors! Is that a typo or I am missing something? Arent' the latter ST velocity vectors (i.e. ST distance over proper time) but not ST displacement vectors (i.e. either time intervals or space intervals)?

Earlier (in #15) , I gave an example with "sound-seconds" (343 meters).
Do you have a problem expressing distances in space using that unit?
A lightning strike in the distance could be described in meters or furlongs or sound-seconds.
Sound-seconds are convenient if use my wristwatch (as opposed to a long tape measure) as my main measuring instrument.
Isn't this how sonar works?

There's no use of invariance or relativity-principle being invoked here.
(Indeed, the speed of sound is not invariant under boosts.)
I just want to use convenient units so that I can draw a diagram and
assign magnitudes to \vec S vectors.
I'm not hiding a distinction between space and time.... I'm demoting the standard SI unit for it.

I understand a sound-second (sonar), just like I understand a light-second (radar). Several issues, however: (i) if you want to use either the speed of sound or the speed of light as conversion factor to turn time units into space units, what is the reason if it is not combining them? (also I assume that we agree that we don't combine them in either dot product or ST displacement intervals, maybe you do this for the purpose of ST velocity intervals, whose utility is pending to be clarified?); (ii) the factor will not be frame-independent or invariant, as you admit; instead Galilean time IS invariant, but by multiplying it by a variant factor you are making it variant, how can it still work in the formulas of a Galilean environment?

Others: thanks for your comments; I understand that you all concur that in Galilean relativity there is no spacetime metric, only a pair of degenerate metrics, one for time and one for space; I gather therefore that in your view the video is wrong in claiming that there is a meaningful Galilean ST displacement vector mixing space and time; in fact I understand that robphy himself does not contradict this specific statement, although he does have a construction coinciding with the video in the desire of introducing smoothly SR, which I am trying to grasp.

 

[robphy]

The spacetime interval that I mentioned (yes, a spacetime displacement vector) is what the author of the video claims to be the invariant interval of Galilean spacetime.

There are some conceptual errors that have to be resolved before we continue.

1. Displacements in spacetime are vectors \vec S=S_t \hat t + S_y \hat y that can be used to move from one point-event to another point-event in a position-vs-time diagram (a spacetime diagram). (Vectors can be scalar-multiplied and added according to the parallelogram rule.)
   https://en.wikipedia.org/wiki/Affine_space
   https://en.wikipedia.org/wiki/Vector_space
2. Vectors on their own have no general notion of magnitude (no specific numerical assignment of a size).
   A dot-product or a metric or something akin to it is additional structure
   that must be specified on top of a vector space.
   https://en.wikipedia.org/wiki/Dot_product
   https://en.wikipedia.org/wiki/Inner_product_space
   
   At a given event, we have a vector space on which we have to specify a rule
   to assign a number to a pair of vectors there.
   If we use the dot product with two copies of the same vector,
   we get a number (called the squared-interval)
   • For a Euclidean dot product (with (x,y)-components), we have \vec S \cdot \vec S\equiv S_x^2+S_y^2\qquad\mbox{Pythagorean thm} The magnitude is the square root: |\vec S|\equiv \sqrt{ \vec S \cdot \vec S }
   • For a Minkowski dot product (with (t,y)-components), we have \vec S \stackrel{M}{\cdot} \vec S\equiv S_t^2-S_y^2
   • For a temporal-Galilean dot product (with (t,y)-components), we have \vec S \stackrel{G}{\cdot} \vec S\equiv S_t^2
     It seems you are concerned with this Galilean dot-product not including in the output number the spatial components of a vector like \vec S. This is what I interpret as
     "the Galilean square-interval not mixing time and space components,
     even though the vector has time and space components".
     
     I don't make any distinction about the nature of any vector.
     So, at this stage, I am not considering 4-velocity vectors.
     (And when I do, it won't matter [with regards to them having time and space components
     and the Galilean dot product not mixing time and space components].
     That one might think of dividing a displacement by a time interval does not affect the mixing description above.)
     

I need this notation and terminology to be clear before proceeding.
Otherwise, there's going to be confusion.

In short,

• Displacement vectors (vectors) are different from squared-intervals (numbers) and intervals (other numbers).
• Displacement vectors have time and space components.
• The temporal-Galilean dot product is a rule that outputs a number
  that does not "mix" (or include both) time and space components (it only has temporal components),
  although the input vectors have time and space components.

 

[Saw]

In short,

• Displacement vectors (vectors) are different from squared-intervals (numbers) and intervals (other numbers).
• Displacement vectors have time and space components.
• The temporal-Galilean dot product is a rule that outputs a number
  that does not "mix" (or include both) time and space components (it only has temporal components),
  although the input vectors have time and space components.

Thanks for taking the time to write all these precisions. I am fine with all of them.

I understand that what you are conveying is the following:

<<Yes, I am considering this displacement spacetime vector, which is a "combination" of space and time components:

\vec S = \color{red}{x{\vec e_x}} + \color{red}{t{\vec e_t}} = \color{blue}{x{\vec e_x}} + \color{blue}{t{\vec e_t}}

But wait, I did not speak yet about "how" these components combine to give us the magnitude of the vector, i.e. I did not yet specify the dot product of this vector space.

In particular, in the Galilean spacetime, although you mention here only the temporal dot product, I think that you will make two different dot products: a spatial one to get the magnitude of a spatial distance and this through vectorial addition of the x, y and z components (as per the Pythagorean Theorem, since they are mutually perpendicular) and a temporal dot product (which in the end is simply the absolute value of the universal time coordinate value). >>

(I must say that I don't give much importance to the intermediate step of the squared interval, because you don't solve "many" problems without taking the square roof thereof...)

Is this more or less reflecting what you wanted to convey?

If so, my comment is only that I don't see much sense in putting time and space together in a vector, if in the end they are not going to join efforts to recombine into the magnitude of the vector in question.

Note again what is the background of my point. If we were to write a dictionary btw math terms and problem-solving language, we'd say that a vector is a problem that you solve by splitting it into smaller problems or clues (components as per a certain basis) whose answers you later recombine into the main problem's solution, pursuant to a certain formula, i..e through a dot product. So it looks weird that you present a problem as potentially solvable through sub-problems time and space, but in the end you leave one of the clues out.

BTW, I must say, to be fair to the author of the reference video, that in the next session, he does admit that there is no sensible Galilean spacetime "distance". In fact, he talks about a ST "separation" vector. The question is still for him, as for you, why you talk about a ST "whatever" vector, containing components that do not combine together in the solution of the problem.

Certainly, if you look at my post #20, I do mention there that problems requiring taking into account both time and space also exist and are solved in the Galilean context, like when you calculate the speed at which you must send a projectile at Event 1 so that it reaches Event 2, given the (variant) time distance and the (invariant) spatial distance between those Events. Still, can you say that here time and space combine as components of a vector? I don't think so...

 

[vanhees71]

---

A useful calculation is to find the eigenvectors

• of the rotation matrix. (There are none.)

A rotation matrix has (at least) one real eigenvalue 1 and a real eigenvector, giving the direction of the rotation axis. That's why the Euclidean spacetime model is not appropriate, because it doesn't admit causal ordering or if you want to enforce causal ordering you have to restrict the rotations, but then the transformations from one inertial frame to another one don't form a group.

 

[PeroK]

@Saw I would try to avoid these long digressions into questions that are of little relevance to the objective - which is, I assume, to learn SR, and ultimately GR.

 

[Saw]

@Saw I would try to avoid these long digressions into questions that are of little relevance to the objective - which is, I assume, to learn SR, and ultimately GR.

Sorry, can you please quote which specific part of my digression is of no relevance to learning SR or GR? Just to know what to take into account in the future.

 

[Saw]

A rotation matrix has (at least) one real eigenvalue 1 and a real eigenvector, giving the direction of the rotation axis.

I was also struck by his statement "none" for eigenvectors of the Euclidean rotation, since there is as you point out an eigenvector constituted by the rotation axis, which (I understand) is the line passing through the fixed point of the rotation, i.e. visually, a line perpendicular to the page where we paint the 2D rotation, right?

But note that in the image that I copied in post #25 from robphy's paper he himself does mention an eigenvector for the Euclidean rotation with coordinates (0,0), corresponding to such perpendicular line?

And another interesting point is what would be the eigenvector of the Galilean boost? In this discussion he mentioned "infinite speed" while in the said paper he mentioned "time". I said that I prefer the second option, although I am not sure if eigenvector would be in this context the accurate term or we are talking about an analog of it.

I think that a parenthesis to clarify this subject would be useful, as it is relevant to the main issue.

 

[PeroK]

Sorry, can you please quote which specific part of my digression is of no relevance to learning SR or GR? Just to know what to take into account in the future.

All of the digression in trying to rework Galilean relativity.

 

[Saw]

All of the digression in trying to rework Galilean relativity.

The very object of the thread? You deem it irrelevant to learning SR and GR? Well, the author of the reference video thinks that his reworking of Galilean relativity makes it easier to understand SR and GR. One of the mentors (robphy) is also very keen on the idea and has made extensive study on that. I am myself fond of the abstract idea (who could not be?, it is obvious that you better understand things by contrast with their close cousins), but I am not so sure about those particular reworkings, about their aptness to better teach SR and GR. I think that this opinion is shared by another mentor, vanhees71.

 

[PeroK]

The very object of the thread?

Yes.

Well, the author of the reference video thinks that his reworking of Galilean relativity makes it easier to understand SR and GR.

He may be right and he may be wrong.

One of the mentors (robphy) is also very keen on the idea and has made extensive study on that.

I didn't say everyone would agree.

 

[vanhees71]

I was also struck by his statement "none" for eigenvectors of the Euclidean rotation, since there is as you point out an eigenvector constituted by the rotation axis, which (I understand) is the line passing through the fixed point of the rotation, i.e. visually, a line perpendicular to the page where we paint the 2D rotation, right?

But note that in the image that I copied in post #25 from robphy's paper he himself does mention an eigenvector for the Euclidean rotation with coordinates (0,0), corresponding to such perpendicular line?

And another interesting point is what would be the eigenvector of the Galilean boost? In this discussion he mentioned "infinite speed" while in the said paper he mentioned "time". I said that I prefer the second option, although I am not sure if eigenvector would be in this context the accurate term or we are talking about an analog of it.

I think that a parenthesis to clarify this subject would be useful, as it is relevant to the main issue.

The null vector never is an eigenvector of any matrix. Because trivially $\hat{A} \vec{0}=\vec{0}$ for any matrix $\hat{A}$.

As I said, for me these pseudo-4D extension is just a convenient way to realize all Galilei transformations (including Galilei boosts) by $4 \times 4$-matrix multiplications, but that's all there is to it. It doesn't add any additional structure to the description of Galilean spacetime than is already there when interpreting it as a fiber bundle, which is the natural choice for the Galilei-Newton spacetime.

Concerning the Galilei boost, let's to for 1D motion. Then the "vector" is
$$\vec{x}=\begin{pmatrix} t \\ x \end{pmatrix}$$
and the boost is described by
$$\vec{x}'=\begin{pmatrix} t \\ x-v t \end{pmatrix}=\begin{pmatrix} 1 & 0 \\ v & 1 \end{pmatrix} \begin{pmatrix} t \\ x \end{pmatrix}.$$
This "Jordan matrix" has only one eigenvector $(0,1)^{\text{T}}$ with eigenvalue $1$, which simply tells you that at time $t=0$ all the points on the $x$ axis are unchanged by the transformation, which is, however trivial anyway.

 

[Saw]

The null vector never is an eigenvector of any matrix. Because trivially $\hat{A} \vec{0}=\vec{0}$ for any matrix $\hat{A}$.

As I said, for me these pseudo-4D extension is just a convenient way to realize all Galilei transformations (including Galilei boosts) by $4 \times 4$-matrix multiplications, but that's all there is to it. It doesn't add any additional structure to the description of Galilean spacetime than is already there when interpreting it as a fiber bundle, which is the natural choice for the Galilei-Newton spacetime.

Concerning the Galilei boost, let's to for 1D motion. Then the "vector" is
$$\vec{x}=\begin{pmatrix} t \\ x \end{pmatrix}$$
and the boost is described by
$$\vec{x}'=\begin{pmatrix} t \\ x-v t \end{pmatrix}=\begin{pmatrix} 1 & 0 \\ v & 1 \end{pmatrix} \begin{pmatrix} t \\ x \end{pmatrix}.$$
This "Jordan matrix" has only one eigenvector $(0,1)^{\text{T}}$ with eigenvalue $1$, which simply tells you that at time $t=0$ all the points on the $x$ axis are unchanged by the transformation, which is, however trivial anyway.

Thanks, for me you are answering the question and would only continue the thread if robphy has more to say.
Just two comments:
- The convenient way to realize the matrix multiplication... does it have to do with "homogeneous coordinates", in the vein of what you can do with a translation? (See my post #12.)
- You may want to put the missing negative sign by the v term in the transformation matrix.

 

[robphy]

A rotation matrix has (at least) one real eigenvalue 1 and a real eigenvector, giving the direction of the rotation axis. That's why the Euclidean spacetime model is not appropriate, because it doesn't admit causal ordering or if you want to enforce causal ordering you have to restrict the rotations, but then the transformations from one inertial frame to another one don't form a group.

The context of this discussion (starting from the OP and the link to eigenchris's YouTube video) has always been on a two-dimensional plane,
and when I joined, I brought up the Cayley-Klein approach
with the parameter E to move between
the Euclidean plane, the (1+1)-Galilean diagram, and the (1+1)-Minkowski diagram.

(This "Spacetime Trigonometry" approach is heavily inspired by
A Simple Non-Euclidean Geometry and Its Physical Basis by I.M. Yaglom
https://www.amazon.com/dp/0387903321/?tag=pfamazon01-20
and modern more mathematical (but less physical) reference is
Perspectives on Projective Geometry: A Guided Tour Through Real and Complex Geometry by Jürgen Richter-Gebert
https://www.amazon.com/dp/3642172857/?tag=pfamazon01-20
)

The null vector never is an eigenvector of any matrix. Because trivially $\hat{A} \vec{0}=\vec{0}$ for any matrix $\hat{A}$.

In relativity, we have null-vectors (nonzero vectors with zero dot-product with itself)
that are not the zero-vector.

One of the mentors (robphy) is also very keen on the idea and has made extensive study on that.

btw.. I'm not a PF mentor.

 

[robphy]

This "Jordan matrix" has only one eigenvector $(0,1)^{\text{T}}$ with eigenvalue $1$, which simply tells you that at time $t=0$ all the points on the $x$ axis are unchanged by the transformation, which is, however trivial anyway.

This Galilean-boost eigenvector corresponds to the limiting infinite speed (infinite slope) of all Galilean-timelike vectors,
similar to the Lorentz-boost eigenvectors corresponding to limiting [finite] velocity of all Minkowski-timelike vectors.

update: The Galilean boost eigenvector also happens to correspond with the concept of "absolute time" because this eigenvector is along the Galilean-circle. Since all tangent vectors to the Galilean circle are parallel, all Galilean observers agree on those events being simultaneous (since the tangents to the circle for each Galilean-4-velocity are Galilean-orthogonal to that 4-velocity).
This is unlike the situation for tangents to a circle (in 2D Euclidean space) and tangents to a hyperbola (in (1+1)-Minkowski spacetime).

The Galilean eigenvalue of 1 means that all Galilean observers will agree on the magnitude of displacement vectors parallel to $(0,1)^{\text{T}}$. Physically, all Galilean observers agree on the length of a ruler. This is "absolute length".

Many results in Galilean geometry are trivial... and since much of the physical interpretations are part of our "common sense", it is difficult to generalize to the non-trivial case without guidance.
The point of my approach is that I am trying to suggest that
many things one learns in "common sense" nonrelativistic physics can be reframed geometrically
to suggest (to provide guidance) to the non-intuitive relativistic physics
(as opposed to the familiar refrain
that I have heard that
one might have to start all over from scratch---
or in the words found in the old video game Marble Madness (and likely elsewhere),
"everything you know is wrong").

Admittedly, the approach is not that easy right now,
since it's unfamiliar.
But I have seen enough parallels in the literature
and now see a way to formalize the analogies and
visualize them with (say) desmos ( https://www.desmos.com/calculator/kv8szi3ic8 )...
so that they are not just cherry-picked...
but that they follow from similar constructions in the three geometries.

So, the reframing is to help build on what one knows (but likely from a different viewpoint)
on the way to special relativity
and beyond (e.g. tensors: http://www.opensourcephysics.org/CPC/posters/salgado-talk.pdf
from http://www.opensourcephysics.org/CPC/abstracts_contributed.html ).

 

[Saw]

btw.. I'm not a PF mentor.

But you mentor people, like me, which is what matters!

Many results in Galilean geometry are trivial... and since much of the physical interpretations are part of our "common sense", it is difficult to generalize to the non-trivial case without guidance.
The point of my approach is that I am trying to suggest that
many things one learns in "common sense" nonrelativistic physics can be reframed geometrically
to suggest (to provide guidance) to the non-intuitive relativistic physics
(as opposed to the familiar refrain
that I have heard that
one might have to start all over from scratch---
or in the words found in the old video game Marble Madness (and likely elsewhere),
"everything you know is wrong").

My interest in the eigenvectors issue has temporarily faded, but you make it revive with this excellent comment. I have names for this phenomenon that you mention, like "backward generalization" or "orphan elements". I mean that an analogy is a one-to-one correspondence between the sets of elements of two or several situations, as well as with the generalized set of elements that embraces all sets. And it often happens that one element looks "orphan" since you don't see its correspondence in the most elementary situation. You don't perceive that connection precisely because it is so "common sense" or "trivial" that you take it for granted. But when you find it, this is most rewarding because it links and thus illuminates both the elementary and the more advanced situations, thanks to this "backward generalization".

This Galilean-boost eigenvector corresponds to the limiting infinite speed (infinite slope) of all Galilean-timelike vectors,
similar to the Lorentz-boost eigenvectors corresponding to limiting [finite] velocity of all Minkowski-timelike vectors.

update: The Galilean boost eigenvector also happens to correspond with the concept of "absolute time" because this eigenvector is along the Galilean-circle. Since all tangent vectors to the Galilean circle are parallel, all Galilean observers agree on those events being simultaneous (since the tangents to the circle for each Galilean-4-velocity are Galilean-orthogonal to that 4-velocity).
This is unlike the situation for tangents to a circle (in 2D Euclidean space) and tangents to a hyperbola (in (1+1)-Minkowski spacetime).

The Galilean eigenvalue of 1 means that all Galilean observers will agree on the magnitude of displacement vectors parallel to $(0,1)^{\text{T}}$. Physically, all Galilean observers agree on the length of a ruler. This is "absolute length".

I understand less the "limiting infinite speed" version of the eigenvector. It is easier to catch the "absolute time" version of the eigenvector and the "absolute length" as eigenvector = 1. If I am not mistaken, this means that the Galilean matrix transformation hinges on the fact that the time vectors remain intact (no change of direction, no change of size), just like the LT of SR hinges on the fact that light vectors experience no change of direction, although they are dilated by Bondi factor... Does this mean that you are assuming measurement of Galilean length with sonar method, as you mentioned in another post?

 

[robphy]

But you mentor people, like me, which is what matters!

Thanks for the vote of confidence.

My interest in the eigenvectors issue has temporarily faded, but you make it revive with this excellent comment. I have names for this phenomenon that you mention, like "backward generalization" or "orphan elements". I mean that an analogy is a one-to-one correspondence between the sets of elements of two or several situations, as well as with the generalized set of elements that embraces all sets. And it often happens that one element looks "orphan" since you don't see its correspondence in the most elementary situation. You don't perceive that connection precisely because it is so "common sense" or "trivial" that you take it for granted. But when you find it, this is most rewarding because it links and thus illuminates both the elementary and the more advanced situations, thanks to this "backward generalization".

Interesting term.
An aspect of some parts of physics is to find patterns from initially-apparently-unrelated ideas.
Some successful unifications include "electricity and magnetism", "terrestrial and universal gravitation", etc...

I understand less the "limiting infinite speed" version of the eigenvector. It is easier to catch the "absolute time" version of the eigenvector and the "absolute length" as eigenvector = 1. If I am not mistaken, this means that the Galilean matrix transformation hinges on the fact that the time vectors remain intact (no change of direction, no change of size), just like the LT of SR hinges on the fact that light vectors experience no change of direction, although they are dilated by Bondi factor...

These conclusions are inspired by seeing corresponding results in the Euclidean and Minkowski cases (sources of some guidance to get from the Galilean case to the Special Relativistic case).

Does this mean that you are assuming measurement of Galilean length with sonar method, as you mentioned in another post?

I'm not sure how the radar-measurements of special relativity
will map down to an analogous procedure that is Galilean invariant.

---

In summary, I think eigenchris' presentation (which I have only glanced at) seems like it is compatible with the Galilean approaches I have been looking at. In some of his other videos, he has done a good job of explaining some ideas that I had difficulty explaining to myself and to others.
So, I think his videos have good value.
...but, yes, it might not be for everyone.

 

[Saw]

In summary, I think eigenchris' presentation (which I have only glanced at) seems like it is compatible with the Galilean approaches I have been looking at. In some of his other videos, he has done a good job of explaining some ideas that I had difficulty explaining to myself and to others.
So, I think his videos have good value.
...but, yes, it might not be for everyone.

I totally agree. As I said from the start for me eigenchris' series is excellent and I also learn a lot from it. I understand that others may be indifferent to this attempt of seeking an analogy among the 3 areas (Euclidean, Galilean, Minkowskian), but I find it most useful, as it illuminates the three of them.

The thing is, however, that I see the analogy working differently from what you and eigenchris claim:

- instead of presenting Galilean time as another basis vector almost on the same footing as the 3 spatial basis vectors, I would precisely remark that Galilean time is not such thing; time is here, instead, as you rightly point out BTW, the eigenvector of the matrix transformation and as such it is an invariant thing, which distinctly differentiates it from that poor variant thing that spatial basis vectors are

- and the shift to SR means that light or, well, to be more accurate, two lightlike (and hence null) vectors take the role of time as eigenvectors, at the cost of time jumping on the wagon of variant things to rub elbows with the 3 spatial basis vectors, as a new basis vector, almost on the same footing as its new brothers, although it keeps a difference in that, when the moment for combination arrives (dot product of the spacetime displacement vector with itself) it is preceded by an opposite sign (though even this should be covered by a generalized expression which is blind to this detail).

I'm not sure how the radar-measurements of special relativity
will map down to an analogous procedure that is Galilean invariant.

Neither do I. I mentioned this only because you did mention a measurement with "sonar" in the context of the discussion about how to make time and space homogeneous...

But I would not dwell more on specific aspects in this post, without testing your interest in more discussion. Certainly, even if you don't agree with my different way of visualizing the analogy as stated above, I find the exchange most useful. If you find it of any use, I would suggest two debates:

- Getting deeper into the issue of what eigenvectors mean and how they operate in each of the 3 areas.
- This issue of conversion btw time and space units, where your views are less clear to me. You and eigenchris (I asked him and he is in your line) see no problem in expressing Galilean time measurements in length units by multiplying the former by an arbitrary speed, which will forcefully be variant, unlike c in SR. We did not advance much in this leg and it deserves discussion.

Apparently, PF does not like long discussions, but I bet this would not be a problem here: some of us (strange people) find analogies fruitful; this particular analogy (with Galilean and Euclidean areas) helps (at least us) to better understand SR and the subject about how this analogy works is not yet peaceful among us.

Also, I would not call this speculation! Say a carpenter has been using a saw for ages and one day he decides to discuss with his colleagues why toothed-things cut wood well, we would not ban the poor guy from learning something from that discussion!

 

[PeroK]

I understand that others may be indifferent to this attempt of seeking an analogy among the 3 areas (Euclidean, Galilean, Minkowskian), but I find it most useful, as it illuminates the three of them.

IMO, this is illuminating:

http://www2.physics.umd.edu/~yakovenk/teaching/Lorentz.pdf

 

[vanhees71]

This Galilean-boost eigenvector corresponds to the limiting infinite speed (infinite slope) of all Galilean-timelike vectors,
similar to the Lorentz-boost eigenvectors corresponding to limiting [finite] velocity of all Minkowski-timelike vectors.

I don't see this infinite limiting speed here. Of course you can get it by a symmetry analysis using the special principle of relativity, homogeneity of time, and Euclidicity of space for all inertial observers as well as the demand that the symmetry transformations must build a group and that the spacetime reconstructed from these symmetry group must admit a "causality structure".

From this analysis you finally get two space-time models: Galilei-Newton spacetime and Minkowski spacetime. The former can, understood in the right way, be interpreted as a deformation of the Minkowski spacetime in the limit of the limiting speed $c \rightarrow \infty$.

The apparent posibility of a Euclidean affine manifold as a spacetime must be abandoned, because it doesn't admit a causality structure.

update: The Galilean boost eigenvector also happens to correspond with the concept of "absolute time" because this eigenvector is along the Galilean-circle. Since all tangent vectors to the Galilean circle are parallel, all Galilean observers agree on those events being simultaneous (since the tangents to the circle for each Galilean-4-velocity are Galilean-orthogonal to that 4-velocity).

Which "Gailean circle"? It's of course true that this analysis uses the concept of absolute time (and in a certain sense also an absolute space) in defining, how the Galilei boosts look like.

You can draw Galilean spactime diagrams much analogous to Minowski spacetime diagrams in SR. Guess, why the former aren't even used by physics-didactics people although they are very much obsessed about the latter ones!

This is unlike the situation for tangents to a circle (in 2D Euclidean space) and tangents to a hyperbola (in (1+1)-Minkowski spacetime).

The Galilean eigenvalue of 1 means that all Galilean observers will agree on the magnitude of displacement vectors parallel to $(0,1)^{\text{T}}$. Physically, all Galilean observers agree on the length of a ruler. This is "absolute length".

Many results in Galilean geometry are trivial... and since much of the physical interpretations are part of our "common sense", it is difficult to generalize to the non-trivial case without guidance.

Galilean geometry is far from trivial. In some sense it's more complicated than Minkowskian geometry, at least concerning the Galilei group vs. the Poincare group when analyzed for their use in QT ;-).

 

[PeroK]

Galilean geometry is far from trivial. In some sense it's more complicated than Minkowskian geometry, at least concerning the Galilei group vs. the Poincare group when analyzed for their use in QT ;-).

And this is the problem. How does a student ever learn SR when they are sidetracked onto the Poincare group before they have touched on the Lorentz Transformation?

 

[vanhees71]

The Lorentz group is a subgroup of the Poincare group. Of course you should study it thoroughly, but without the spactime translations you'll have a hard time to construct the dynamics of relativistic QT.

 

[PeroK]

The Lorentz group is a subgroup of the Poincare group. Of course you should study it thoroughly, but without the spactime translations you'll have a hard time to construct the dynamics of relativistic QT.

How much Group Theory does the OP know?

 

[robphy]

This Galilean-boost eigenvector corresponds to the limiting infinite speed (infinite slope) of all Galilean-timelike vectors,
similar to the Lorentz-boost eigenvectors corresponding to limiting [finite] velocity of all Minkowski-timelike vectors.

I don't see this infinite limiting speed here. Of course you can get it by a symmetry analysis using the special principle of relativity, homogeneity of time, and Euclidicity of space for all inertial observers as well as the demand that the symmetry transformations must build a group and that the spacetime reconstructed from these symmetry group must admit a "causality structure".

Consider an analogue for a power iteration method for attempting the computation of an eigenvector of a matrix.
Repeatedly applying a Galilean-boost to a Galilean 4-velocity,
\left( \begin{array}{cc}<br /> 1 &amp; 0 \\<br /> v &amp; 1<br /> \end{array} \right)^n<br /> \left( \begin{array}{c}<br /> 1 \\<br /> u<br /> \end{array} \right)<br /> =\left( \begin{array}{c}<br /> 1 \\<br /> nv+u<br /> \end{array} \right)<br />
tends to a Galilean 4-velocity with unbounded speed as n\rightarrow \infty.

You can draw Galilean spactime diagrams much analogous to Minowski spacetime diagrams in SR. Guess, why the former aren't even used by physics-didactics people although they are very much obsessed about the latter ones!

Every introductory physics textbook draws a Galilean spacetime diagram ( a position-vs-time graph ),
although they probably don't know that.

Many results in Galilean geometry are trivial... and since much of the physical interpretations are part of our "common sense", it is difficult to generalize to the non-trivial case without guidance.

Galilean geometry is far from trivial. In some sense it's more complicated than Minkowskian geometry, at least concerning the Galilei group vs. the Poincare group when analyzed for their use in QT ;-).

Yep, I agree.
That's why I said "Many results in Galilean geometry are" and not "Galilean geometry is".
Some aspects (like the degenerate properties of the metrics) introduce complications not seen in the Euclidean and the Minkowski case.

 

[vanhees71]

Consider an analogue for a power iteration method for attempting the computation of an eigenvector of a matrix.
Applied to a Galilean 4-velocity,
\left( \begin{array}{cc}<br /> 1 &amp; 0 \\<br /> v &amp; 1<br /> \end{array} \right)^n<br /> \left( \begin{array}{c}<br /> 1 \\<br /> u<br /> \end{array} \right)<br /> =\left( \begin{array}{c}<br /> 1 \\<br /> nv+u<br /> \end{array} \right)<br />
tends to a Galilean 4-velocity with unbounded speed as n\rightarrow \infty.Every introductory physics textbook draws a Galilean spacetime diagram ( a position-vs-time graph ),
although they probably don't know that.

That's not a Galilean spacetime diagram depicting two different inertial frames.

I once did this for curiosity. The result is

I think it's really good for nothing, confusing the simple formulae of the Galilei transformation even more than the Minkowski diagram for the somewhat more complicated formulae of the Lorentz transformation.

 

[Saw]

That's not a Galilean spacetime diagram depicting two different inertial frames.

I once did this for curiosity. The result is

View attachment 321007
I think it's really good for nothing, confusing the simple formulae of the Galilei transformation even more than the Minkowski diagram for the somewhat more complicated formulae of the Lorentz transformation.

In a similar attempt, I have drawn this, which tries to convey that the different vertical positions that the origins O and O take at each instant do not constitute, strictly speaking, different time axes. The timeline is a different thing that does not form part of the "basis" just like the lightlike vectors being the eigenvectors in SR.

 

[robphy]

That's not a Galilean spacetime diagram depicting two different inertial frames.

But it is. You (and likely many others) just don't see it and maybe don't appreciate it.
Maybe the situation is uninteresting to you.

(For comparisons with standard position-vs-time diagrams and xy-axes in the Euclidean plane,
the time axes below all run horizontally to the right. I use "y" for space in the spacetime diagrams.)

From earlier...

Here's a more interesting application:
Rolling without slipping as a superposition of motions in two reference frames.
Though one need not actively invoke or recognize the underlying Galilean geometry,
it is implicitly being used.

I once did this for curiosity. The result is

View attachment 321007
I think it's really good for nothing, confusing the simple formulae of the Galilei transformation even more than the Minkowski diagram for the somewhat more complicated formulae of the Lorentz transformation.

I acknowledge your opinion.

Sometimes things (even apparently silly and useless things, at first glance) are done for practice,
in preparation for more complicated operations.

"Paint the fence"

Sometimes one needs to see it in comparison to the other E-alternatives,
like in time dilation and length contraction
(as in my https://www.desmos.com/calculator/kv8szi3ic8 and in my poster linked above https://www.aapt.org/doorway/Posters/SalgadoPoster/Salgado-GRposter.pdf ).

These diagrams suggest (in hindsight) that Galilean is an intermediate geometry.
With guidance, one can be led to Special Relativity
(as in the Parable that I wrote attached to the end of the poster where

• a Galilean tries to interpret a position-vs-time graph geometrically
  in the spirit of Euclidean geometry with an experimentally determined circle on that diagram (where arc-lengths of worldlines are measured by wristwatches)
• then Minkowski (with improved experimentation) determines a more realistic circle on that diagram.

)