sdfsfasdfasf
- 75
- 12
- Homework Statement
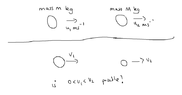
- If two particles collide (with coefficient of restitution between 0 and 1), is it possible for the first particle to have a speed less than the second particle (and be not have its direction of motion changed)?
- Relevant Equations
- Conservation of linear momentum
separation / approach = e
I am stuck with this problem.
Intuition tells me the answer is no, but I am struggling to prove it.
If we consider two particles travelling in the same direction, the 2nd particle will gain velocity (impulse is in same direction to velocity), and the first particle will lose velocity (if it finishes with v>0 then its direction of motion is unchanged, yet its going slower than it was), if v<0 then it clearly goes in the other direction. Is it possible for the 1st particle to slow down so little that it ends up going faster than the 2nd one?
In either case, if 1st particle left with less velocity than 2nd (but didn't change direction of motion ) then there would be an immediate second collision (this is what is making me apprehensive).
Help appreciated, thanks for reading.
Intuition tells me the answer is no, but I am struggling to prove it.
If we consider two particles travelling in the same direction, the 2nd particle will gain velocity (impulse is in same direction to velocity), and the first particle will lose velocity (if it finishes with v>0 then its direction of motion is unchanged, yet its going slower than it was), if v<0 then it clearly goes in the other direction. Is it possible for the 1st particle to slow down so little that it ends up going faster than the 2nd one?
In either case, if 1st particle left with less velocity than 2nd (but didn't change direction of motion ) then there would be an immediate second collision (this is what is making me apprehensive).
Help appreciated, thanks for reading.
Last edited: