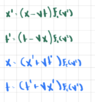zenterix
- 774
- 84
- TL;DR Summary
- When deriving the Lorentz transformation, it seems we can pick specific functions to be used in the equations. If we choose functions that lead to a slightly different transformation, what do we make of this transformation?
Susskind's book "Special Relativity and Classical Field Theory" derived the Lorentz transformations
$$x'=(x-vt)\frac{1}{\sqrt{1-v^2}}$$
$$t'=(t-vx)\frac{1}{\sqrt{1-v^2}}$$
$$x=(x'+vt')\frac{1}{\sqrt{1-v^2}}$$
$$t=(t+vx')\frac{1}{\sqrt{1-v^2}}$$
While redoing the calculations, I reached a point where it seems to me I could choose the transformation to be
$$x'=x-vt$$
$$t'=t-vx$$
$$x=(x'+vt')\frac{1}{1-v^2}$$
$$(t'+vx')\frac{1}{1-v^2}$$
Are these latter four equations also Lorentz transformations?
I'm going to post here my exact calculations to reach these equations.
I started with a stationary frame A (coordinates x and t) and a moving frame B (coordinates x' and t', with three railcars)
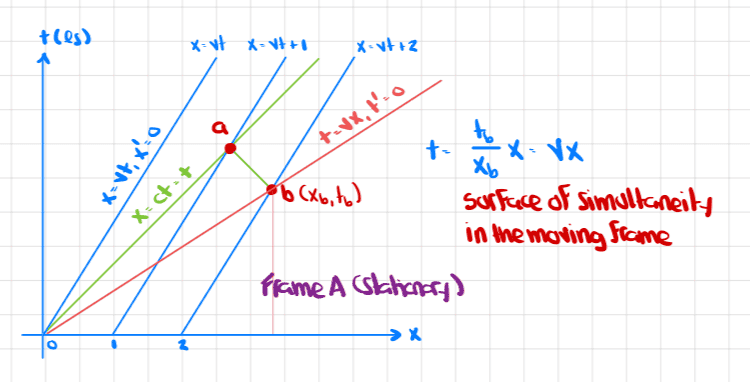
From this scenario we conjecture a transformation of the form
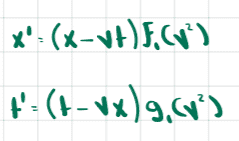
But then what if we think about frame B being stationary and the three railcars being in frame A (which is now moving relative to frame B). We have
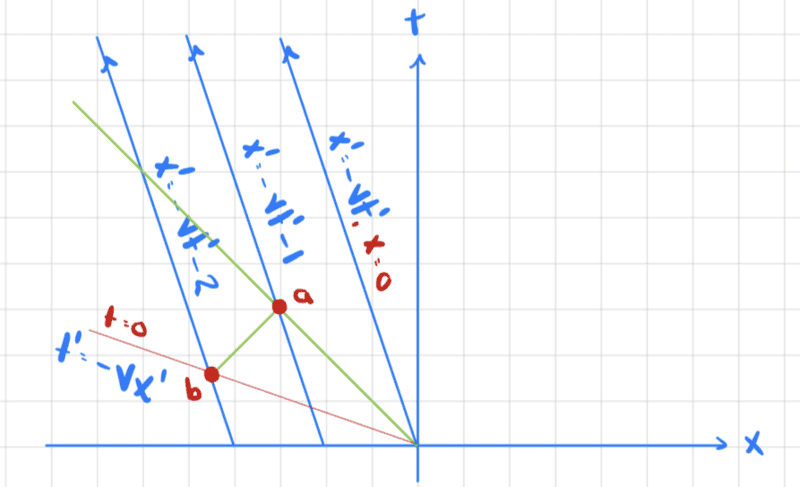
Here are the calculations to find points a and b
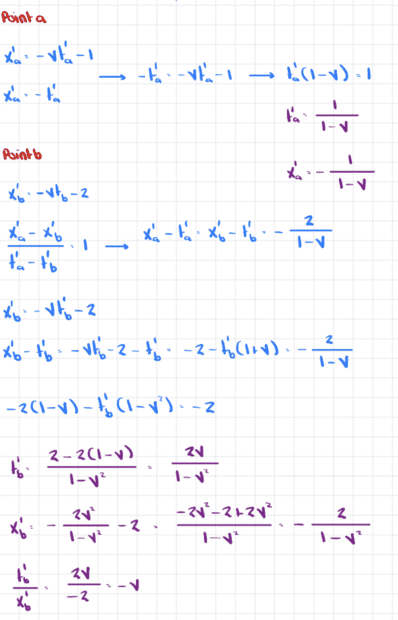
So we conjecture that the transformation from coordinates in frame A to frame B are
$$x=(x'+vt)f_2(v^2)$$
$$t=(t'+vx')g_2(v^2)$$
At this point, taking into consideration the four equations that we have conjectured, we have
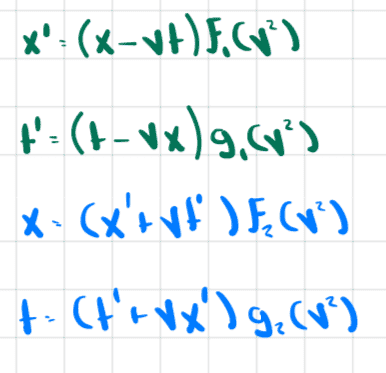
But we can show that ##f_1=g_1## and ##f_2=g_2## by considering the fact that a light ray has equations
$$x=t$$
$$x'=t'$$
Thus,
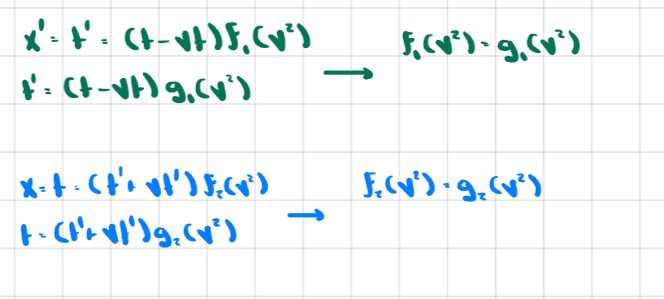
Hence our equations become
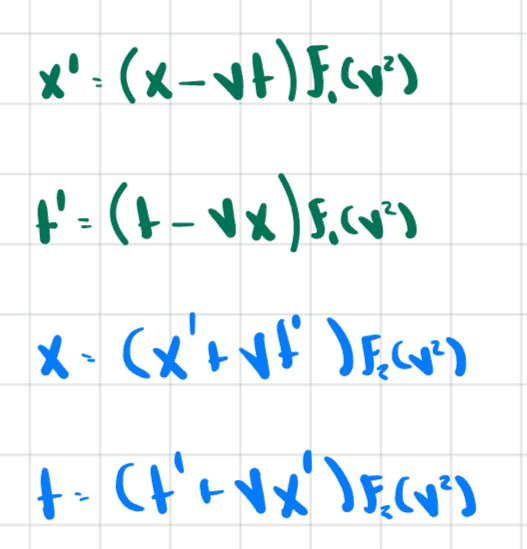
And now if we solve for ##f_1## or ##f_2## we obtain
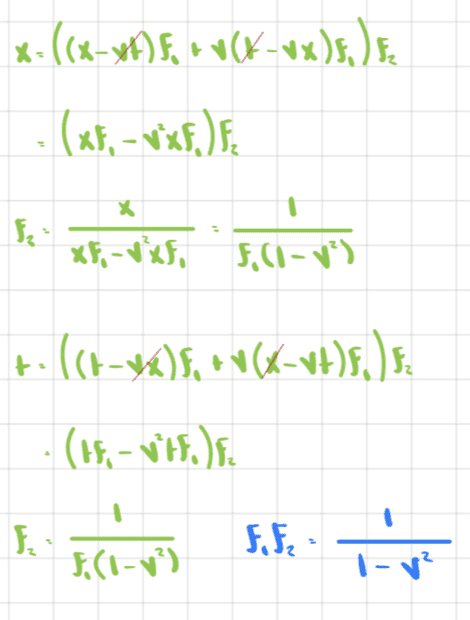
One option is to say ##f_1=f_2## and then we obtain the usual Lorentz transformation.
But can we not choose other functions?
For example suppose ##f_1=1## and ##f_2=\frac{1}{1-v^2}##. Then we get
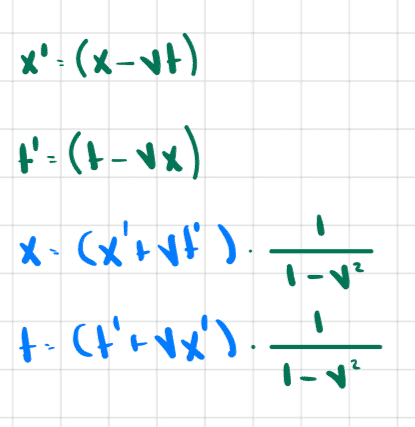
$$x'=(x-vt)\frac{1}{\sqrt{1-v^2}}$$
$$t'=(t-vx)\frac{1}{\sqrt{1-v^2}}$$
$$x=(x'+vt')\frac{1}{\sqrt{1-v^2}}$$
$$t=(t+vx')\frac{1}{\sqrt{1-v^2}}$$
While redoing the calculations, I reached a point where it seems to me I could choose the transformation to be
$$x'=x-vt$$
$$t'=t-vx$$
$$x=(x'+vt')\frac{1}{1-v^2}$$
$$(t'+vx')\frac{1}{1-v^2}$$
Are these latter four equations also Lorentz transformations?
I'm going to post here my exact calculations to reach these equations.
I started with a stationary frame A (coordinates x and t) and a moving frame B (coordinates x' and t', with three railcars)
From this scenario we conjecture a transformation of the form
But then what if we think about frame B being stationary and the three railcars being in frame A (which is now moving relative to frame B). We have
Here are the calculations to find points a and b
So we conjecture that the transformation from coordinates in frame A to frame B are
$$x=(x'+vt)f_2(v^2)$$
$$t=(t'+vx')g_2(v^2)$$
At this point, taking into consideration the four equations that we have conjectured, we have
But we can show that ##f_1=g_1## and ##f_2=g_2## by considering the fact that a light ray has equations
$$x=t$$
$$x'=t'$$
Thus,
Hence our equations become
And now if we solve for ##f_1## or ##f_2## we obtain
One option is to say ##f_1=f_2## and then we obtain the usual Lorentz transformation.
But can we not choose other functions?
For example suppose ##f_1=1## and ##f_2=\frac{1}{1-v^2}##. Then we get