Can We Construct a Triangle with Given Lengths and Find Its Area?

[Albert1]

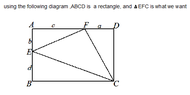
$a,b,c,d >0$,
please prove we can construct an triangle with length:
$\sqrt{b^2+c^2},\sqrt{a^2+c^2+d^2+2ac},\sqrt{a^2+b^2+d^2+2bd}$
and find the area of the triangle

 

[RLBrown]

Spoiler

Let
Q1 = b^2 + c^2;
Q2 = a^2 + c^2 + d^2 + 2 a c;
Q3 = a^2 + b^2 + d^2 + 2 b d;

Using: 16 Area^2 = Archimedes[ Q1, Q2, Q3]

I get
Area = $$\frac{1}{4} \sqrt{4 \left(b^2+c^2\right) \left(a^2+2 a c+c^2+d^2\right)-\left(2 a^2+2 a c+2 b^2+2 b d+2 c^2+2 d^2\right)^2}$$

 

[Albert1]

hint:

Spoiler

View attachment 4472

 

[RLBrown]

Spoiler

Removing triangle areas from rectangle:

ABCD = (a + c) (b + d);
AEF = c b/2;
DCF = a (b + d)/2;
BCE = d (a + c)/2;
A = ABCD - AEF - DCF - BCE
FullSimplify[A]

A = $\frac{1}{2} (a b+c (b+d))$

 

[RLBrown]

Spoiler

Let
Q1 = b^2 + c^2;
Q2 = a^2 + c^2 + d^2 + 2 a c;
Q3 = a^2 + b^2 + d^2 + 2 b d;

Using: 16 Area^2 = Archimedes[ Q1, Q2, Q3]

I get
Area = $$\frac{1}{4} \sqrt{4 \left(b^2+c^2\right) \left(a^2+2 a c+c^2+d^2\right)-\left(2 a^2+2 a c+2 b^2+2 b d+2 c^2+2 d^2\right)^2}$$

Miss Application of Archimedes Formula:
CORRECTION:

Spoiler

Q1=b^2+c^2;
Q2=a^2+c^2+d^2+2 a c;
Q3=a^2+b^2+d^2+2 b d;
Arc = 4 Q1 Q2 -( Q1+ Q2-Q3 )^2
$$\text{FullSimplify}\left[\sqrt{\frac{\text{Arc}}{16}}\right]$$
$$\frac{1}{2} (a b+c (b+d))$$