mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
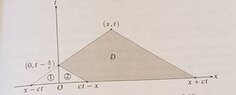
I want to verify that $$w(x,t)=\frac{1}{2c}\int_0^t\int_{c(t-\tau)-x}^{x+c(t-\tau)}f(y,\tau)dyd\tau$$ is the solution of the problem $$w_{tt}=c^2w_{xx}+f(x,t) , \ \ x>0, t>0 \\ w(x,0)=w_t(x,0)=0, \ \ x>0 \\ w(0,t)=0 , \ \ t\geq 0$$ For that we have to take the partial derivatives of $w$. But how can we do that in this case for example as for $t$ where we have at both integrals the $t$ ? Could you give me a hint? (Wondering)
I want to verify that $$w(x,t)=\frac{1}{2c}\int_0^t\int_{c(t-\tau)-x}^{x+c(t-\tau)}f(y,\tau)dyd\tau$$ is the solution of the problem $$w_{tt}=c^2w_{xx}+f(x,t) , \ \ x>0, t>0 \\ w(x,0)=w_t(x,0)=0, \ \ x>0 \\ w(0,t)=0 , \ \ t\geq 0$$ For that we have to take the partial derivatives of $w$. But how can we do that in this case for example as for $t$ where we have at both integrals the $t$ ? Could you give me a hint? (Wondering)