lioric
- 335
- 26
- TL;DR Summary
- A student of mine came and said that their teacher said that they were to use the coordinates of the point of tendency as one of the coordinates to find gradient.
We were taught to take coordinates like this
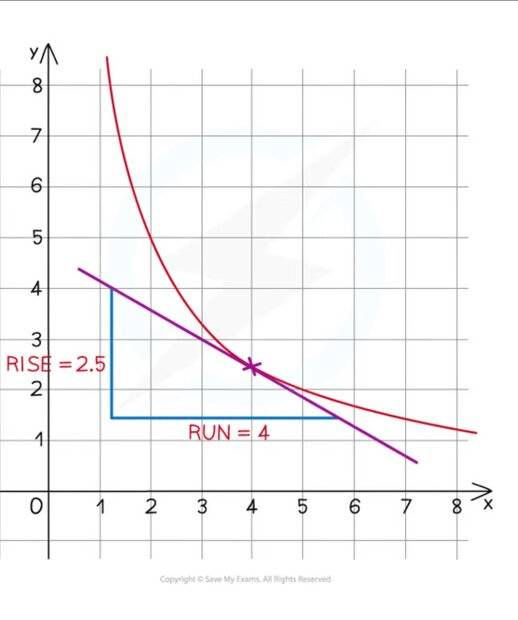
But teacher is telling the student to take coordinates like this. What are the major reasons why this is not taught like this. I know the value would be the same, but I also know there is a reason why we don't use this method.
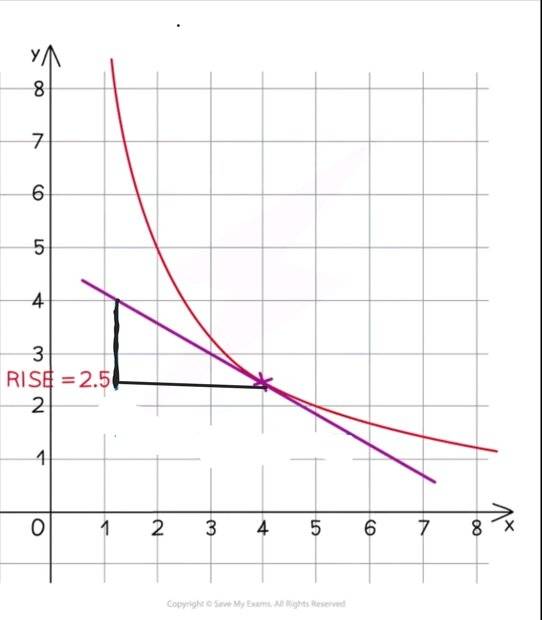
But teacher is telling the student to take coordinates like this. What are the major reasons why this is not taught like this. I know the value would be the same, but I also know there is a reason why we don't use this method.