Can you please draw this question's figure for me?

[vkash]

Homework Statement

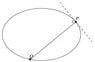
From a point P tangent drawn to ellipse $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$. If the chord of contact is normal to the ellipse, then find the locus of P.

I think this is impossible.. Most probably i am drawing it wrong. that's why i am asking so please draw it so that i complete this question.
Just draw figure after that i will try to do it by self

 

[HallsofIvy]

What do you mean by "chord of contact"?

 

[vkash]

What do you mean by "chord of contact"?

If you draw a tangent from a point (outside curve), there will two such tangents. so you will get two points of contact of tangents on the curve.join these two points you will get chord of contact.
There are many examples see here

 

[Mark44]

And what does "normal to the ellipse" mean?

 

[vkash]

And what does "normal to the ellipse" mean?

see image
line PQ is normal to ellipse at p

 

[HallsofIvy]

P is the point on the ellipse? Then I don't understand "find the locus of P". The "chord of contact", which appears to be the chord perpendicular to the tangent, is tangent at P, by definition, for all P. Or are you requiring that it be perpendicular to the ellipse at the other intersection? That can happen only at the vertices.

 

[vkash]

P is the point on the ellipse? Then I don't understand "find the locus of P". The "chord of contact", which appears to be the chord perpendicular to the tangent, is tangent at P, by definition, for all P. Or are you requiring that it be perpendicular to the ellipse at the other intersection? That can happen only at the vertices.

I think you are confused by the last image i upload. That is for telling Mark that what is normal.I download that from Google images to show mark, don't confused with that image.

 

[verty]

Well I can draw the figure but I am stumped as to how to find the locus.

Just add a tangent at Q in the sketch above, then you have two tangents that meet in a point, and their chord of contact is normal to the ellipse.

 

[vkash]

Well I can draw the figure but I am stumped as to how to find the locus.

Just add a tangent at Q in the sketch above, then you have two tangents that meet in a point, and their chord of contact is normal to the ellipse.

if chord of contact is normal to ellipse. then it will normal to the tangent at that point on ellipse.
if at the both ends of the chord of contact it is perpendicular to tangent then how they can meet.
Just draw it's rough sketch.
It is solved question but even after watching the solution i have not found the real figure.
verty if you know figure then please draw it.

 

[verty]

Well if, as you say, it is impossible for two tangents to meet that are both orthogonal to the chord of contact, and the question asks for the locus of points where two tangents meet, they aren't talking about the same tangents.

So they are talking about the case I described, the chord is normal at one point.

 

[vkash]

i didn't understand question's language.
It is normal question.

Well I can draw the figure but I am stumped as to how to find the locus.

Just add a tangent at Q in the sketch above, then you have two tangents that meet in a point, and their chord of contact is normal to the ellipse.

see answer image is in attachment not good image but you can understand what's answer.
In answer two equations of chord of contact are compared.

so finally problem solved.(That's confusion).
Thanks to all the persons who reply.

 

[verty]

I don't know what $S_1$ means and I don't understand the last step. I like easy questions with known strategies, this is just too advanced. Probably it makes sense if one studies from the textbook that you got that from, or those listed in the prerequisites.

Best of luck.