Can you read my English on 4 colour theorem?

[fenstip]

line-node-map is formed by lines and nodes, commonly used by the one (including me) who reseaches four colour theorem.

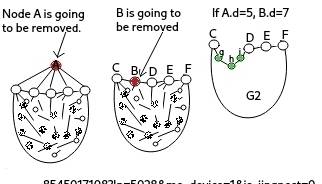
Smallest five colours map is the one with fewest number of nodes and couldn't be coloured less than five colours, and also, it can be a complete map by adding lines not nodes. I remove temporarily two adjacent nodes (A and B) from the map, now, the colours (or after re-colour) on the nodes of the map are 1,2,3,4 or less. The map at the above showing just the nodes at the very edge (rim? outside?) of the map (there are still other patterns to consider), then if I could change the colour on some of them in my way, and put back A and B, the map is four colours. I put some Kempe Chain to the current nodes which are at the edge, then I'm not going to change their colours because it's difficult. But the Kempe Chain blocks other connections, that's the point I can use.

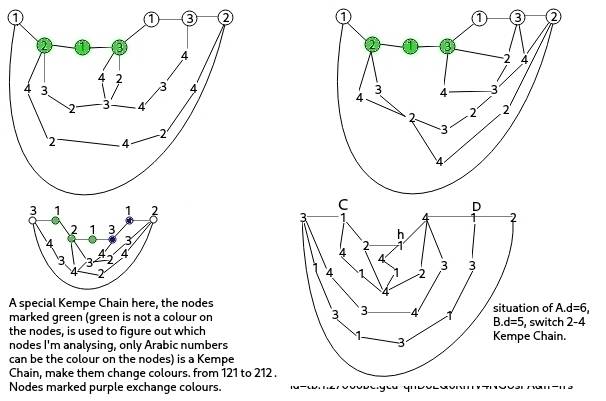
Assuming A.c=5 (colour of A), A.d=5 (degree(s) or how many node(s) connecting to), B.d=6, after removing AB, the nodes at the edge are CghiDEF (other nodes are existed in the map but I didn't have them shown due to convenience). Remove AB from the map, call that map G2. Supposed C.c=1, g.c=2, h.c=1, i.c=3, D.c=1, E.c=3, F.c=2, if there is no Kempe chain between g and F, I will change g.c to 4, causing B.d=6 impossible. But to consider fully, I have to set a Kempe chain between g and F, the same reason, Kempe chain between gi, iE, just an example. After that the Kempe Chain block C,h to genarate 1-3 an 1-4 Kempe Chain, so I change C.c to 3, (it may generate 3-2 between between i, and so on but this couln't stop colour change), change D.c to 3. Now, put back AB, map is four colours. So the best way to keep the asumption is to set B.d 7 or above. Now, do the same thing to DEF.

Sorry if my English has you confused.

 

[jedishrfu]

Sadly, your English description of the 4 color problem is very confusing.

What are you trying to say? are you attempting to construct a 5 color solution or find a map that can't be colored by 4 colors?

It looks like you're trying to develop an algorithm that can take an n color map and reduce it to a 4 color map and that you're using a 5 color map as an example.

 

[fenstip]

Sadly, your English description of the 4 color problem is very confusing.

What are you trying to say? are you attempting to construct a 5 color solution or find a map that can't be colored by 4 colors?

It looks like you're trying to develop an algorithm that can take an n color map and reduce it to a 4 color map and that you're using a 5 color map as an example.

I had forgot to tell you that this is just a first part of my proof. You are almost right, I try to construct 5 colors map, and try to find the rules of degree on a node, and at last no map can match that node.d. But I was not sure you can read my english, but you can guess some of my mind. I guess if my writing is long and wrong will make you blame me.

 

[jedishrfu]

Please be aware that we don't tend to discuss original work by anyone. We do discuss work that has been published in a reputable peer-reviewed math journal.

 

[jedishrfu]

The 4 color proof was first done by computer trying out all cases.

https://en.m.wikipedia.org/wiki/Four_color_theorem

Successive proofs relied on computer support as well.

 

[fenstip]

I will reduce the number of examples or patterns by V-merge.

Erase all colours on the map, pull and drag C,h together by extending the lines to C,h, that will merge C,h to form a node called V1, the same reason, merge V1 and D to form V2, right now there are two nodes less, so after putting colours on the map, can be only four or even less colours. Splitting the V2 node from the map, V1 and D have the same colour, then split V1, Ch has the same colour, all colours at the map maybe four, or within. Good news is 3 nodes (ChD) when A.d=5 have the same colour.

Also, I can do the same thing to patterns (A.d=5,B.d=5). A.d>=7 is easy to deal with by setting connected node.d to >= 5 due to <5 is impossible to keep the assume, And some of the Kempe Chains have the different end points, lengths, breaking through other area rounded by other kempe chain, like Kempe Chain between gi goes through Kempe Chain between iE. I think it's easy to get rid of these situations. If I'm wrong, you are easy to tell like P.J.Heawood because I heavily use Kempe Chain.

If A.d=6 in the map, not to remove B. After V-merge,the map looks like G3

,
Three nodes have the same color, adding Kempe Chain could not stop the color change. So the best option for 5 color map is A.d=6 doesn't existed.

If the above proof is right, then the rules are: if A.d is 5, then the nodes.d connected to A is >= 7. if A.d>=7, then the nodes.d connected to A is equal to or more than 5.

 

[fenstip]

G3 and its referring proof is wrong, A.d=6 won't be ignored in my later proof.

G3 and its referring proof is wrong, A.d=6 won't be ignored in my later proof.

 

[berkeman]

Thread closed for Moderation...

 

[fresh_42]

There has been long and intensive research for a proof of the 4-color-theorem, before a proof finally had been published, including the automatic check of many cases. Many high-profile topologists have worked on the problem. This means, that it is extremely unlikely that anyone else finds a shorter version, or even a version that does not require manual checks for exceptional cases.

Please be aware that we don't tend to discuss original work by anyone. We do discuss work that has been published in a reputable peer-reviewed math journal.

The 4 color proof was first done by computer trying out all cases.

https://en.m.wikipedia.org/wiki/Four_color_theorem

Successive proofs relied on computer support as well.

There is nothing left to add.

The thread remains closed.